Una mini-serie a cura di Gabriele Belegni, dove esploreremo i concetti principali di una delle branche più affascinanti della matematica: la topologia. Cercheremo di scoprire le motivazioni e le idee che hanno spinto ad introdurre certi concetti concentrandoci sull’aspetto intuitivo piuttosto che su quello formale. Questa volta tratteremo delle proprietà capaci di catturare informazioni sugli spazi topologici, fornendone una sorta di identikit. Trovate tutte le puntate su questa pagina.

Facciamo un brevissimo riassunto delle scorse puntate: abbiamo detto che la topologia si occupa di capire se, dati due spazi topologici, essi sono omeomorfi o no o, letto in termini informali, se due oggetti possono essere deformati l’uno nell’altro in maniera continua, senza dover commettere strappi o cuciture (“omeomorfismo” è il termine matematico per queste deformazioni, e se esiste un omeomorfismo tra due spazi diremo che essi sono omeomorfi). Per dire che due spazi topologici sono omeomorfi basta trovare un omeomorfismo tra di essi, cioè una funzione continua, invertibile e con inversa continua, e questo di solito non crea troppi problemi. Le cose diventano fastidiose quando vogliamo provare che due spazi non sono omeomorfi. Stando alla definizione dovremmo provare che non esiste nessun omeomorfismo tra di essi, dovremmo cioè andare a controllare tutte le possibili funzioni di uno spazio nell’altro (e fidatevi, sono tante) e verificare che nessuna di esse soddisfa tutte le richieste per essere omeomorfismo. Un’impresa del genere è semplicemente improponibile, va dunque cercata un’altra strada.

Come fare? Beh vediamo. In topologia due spazi omeomorfi sono in un certo la stessa cosa, dovranno quindi avere qualcosa che li renda simili, alcune proprietà in comune. Sembra sensato, ma questo come ci aiuta? L’idea è la seguente: se riuscissimo a trovare delle proprietà che sono necessariamente condivise da spazi omeomorfi, per provare che due spazi non sono omeomorfi basterebbe far vedere che non condividono alcune di queste proprietà. Le chiameremo proprietà topologiche.

Formalmente, diciamo che \(P\) è una proprietà topologica se, dati due spazi topologici \(X\) e \(Y\) tali che \(X\) soddisfa la proprietà \(P\) ma \(Y\) non la soddisfa, allora \(X\) e \(Y\) non sono omeomorfi. Letta al contrario, se \(X\) e \(Y\) sono omeomorfi e uno dei due ha la proprietà \(P\), allora anche l’altro deve avere la proprietà \(P\). Badate bene, se due spazi condividono una proprietà topologica non è detto che essi siano omeomorfi, ma se non la condividono allora sicuramente non sono omeomorfi. È un punto sottile ma molto importante.

Ci sono molte proprietà topologiche, oggi ve ne mostrerò solo alcune.

Partiamo con quella a mio parere più intuitiva. Due spazi omeomorfi possono essere deformati uno nell’altro senza commettere strappi o cuciture: nel concreto, uno strappo può andare ad aumentare il numero di pezzi di cui uno spazio è costituito, mentre una cucitura va a diminuire questo numero, e l’unico modo per aumentare e diminuire il numero di pezzi di uno spazio è proprio strapparlo o cucirne parti distinte. Di conseguenza spazi omeomorfi dovranno necessariamente essere costituiti da uno stesso numero di pezzi. Il nome tecnico per questi “pezzi” è componenti connesse, e il numero di componenti connesse è una proprietà topologica: se due spazi hanno un diverso numero di componenti connesse, per passare da uno all’altro dovrò necessariamente incollare o strappare qualcosa, e quindi essi non possono essere omeomorfi.

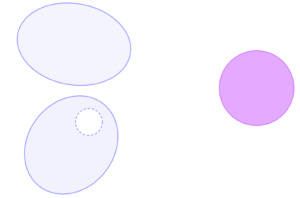  Lo spazio azzurro, a sinistra, ha 2 componenti connesse, mentre la boccia unitaria (in viola), a destra, ha una sola componente connessa.
Di conseguenza, questi due spazi non sono omeomorfi.

La proprietà topologica forse più utile nelle applicazioni è la compattezza: al di là della definizione formale, pensate a uno spazio compatto come a uno spazio che generalizza gli insiemi finiti, cioè ad uno spazio infinito ma che condivide alcune proprietà comode degli insiemi finiti o, se volete, a uno spazio a cui non mancano particolari punti, non ha “buchetti”, appunto è compatto.

Ancora meglio, uno spazio compatto può essere visto come la generalizzazione degli insiemi chiusi e limitati di \(\mathbb{R}^n\) (lo spazio a \(n\) dimensioni). Molti di voi ricorderanno che negli insiemi chiusi e limitati di \(\mathbb{R}^n\) valgono vari teoremi interessantissimi e utilissimi in analisi matematica, ad esempio il teorema di Weierstrass, di Heine-Cantor e di Bolzano-Weierstrass (se non li conoscete, tranquilli, non sono necessari alla discussione, basti sapere che sono veramente utili in analisi). Ecco, tutti questi bei teoremi continuano a valere nel contesto più generale degli spazi compatti, e in matematica ci piace molto quando qualcosa si generalizza, perché possiamo applicarlo a tante situazioni in più!
Tenete sempre a mente che dentro \(\mathbb{R}^n\) gli spazi compatti sono tutti e soli quelli chiusi e limitati (per capirci, una retta ed un semipiano sono illimitati, mentre un segmento o un quadrato sono limitati), e in particolare \(\mathbb{R}^n\) stesso non è compatto in quanto non è limitato.

In uno spazio compatto ho un forte controllo sui limiti e sulle successioni, che sono gli strumenti su cui si fonda praticamente tutta l’analisi, e quindi le funzioni (soprattutto quelle continue) si comportano bene in questi spazi, non assumono un comportamento incontrollabile, non possono schizzare e assumere valori infiniti da nessuna parte. In particolare, se stiamo lavorando in uno spazio metrico compatto allora ogni successione ha un punto di accumulazione, cioè un punto attorno a cui si trovano infiniti elementi della successione, appunto vi si accumulano (ricordate, uno spazio metrico è uno spazio topologico dove sappiamo misurare le distanze); in questo senso uno spazio compatto non ha “buchetti”, non gli mancano singoli punti che potrebbero essere il limite di qualche successione.

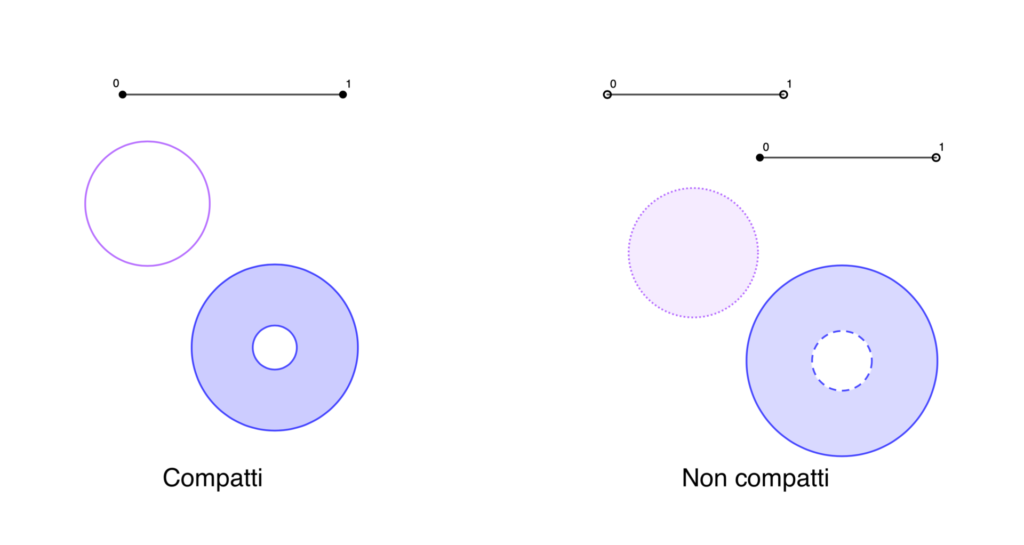L’intervallo unitario, la circonferenza \(S^1\) e un anello circolare “con buco chiuso” sono compatti, mentre l’intervallo senza uno o più punti (estremi o non), la boccia aperta e un anello circolare “con buco aperto” non sono compatti. Alla boccia aperta e all’anello circolare con buco aperto mancano i punti del bordo, e quindi una successione che tende al bordo non ha limite, cosa che non accade negli esempi di spazi compatti.

Grazie alla compattezza possiamo ad esempio provare che la circonferenza unitaria \(S^1\) ed il piano \(\mathbb{R}^2\) non sono omeomorfi, in quanto \(S^1\) è compatto mentre \(\mathbb{R}^2\) non lo è, e in effetti sembra impossibile deformare l’intera circonferenza su un piano senza strappare o incollare nulla. Analogamente un segmento chiuso ed una semiretta non sono omeomorfi, e non lo sono nemmeno un disco con bordo ed uno senza bordo.

Le ultime proprietà topologiche che voglio mostrarvi riguardano come gli aperti “separano” i punti dello spazio. Ora mi spiego.

Diciamo che uno spazio è \(T_1\) se, dati due suoi punti \(x\) e \(y\), esistono due aperti \(A\) e \(B\) tali che \(A\) contiene \(x\) ma non \(y\) e \(B\) contiene \(y\) ma non \(x\).
Uno spazio è \(T_2\) (anche detto di Hausdorff) se vale la stessa cosa che negli spazi \(T_1\) ma, in aggiunta, gli aperti \(A\) e \(B\) sono disgiunti tra loro (in un certo senso, gli aperti “separano” i punti meglio che negli spazi \(T_1\)).
Uno spazio è \(T_3\) se è \(T_1\) e, dato un qualunque punto \(x\) ed un chiuso \(C\) che non lo contiene, esistono 2 aperti \(A\) e \(B\) tali che \(A\) contiene \(x\), \(B\) contiene \(C\) e \(A\) e \(B\) sono disgiunti.
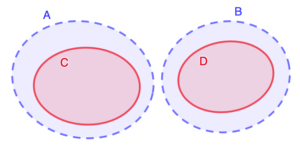
Infine, uno spazio è \(T_4\) se è \(T_1\) e, dati due chiusi disgiunti \(C\) e \(D\), esistono due aperti disgiunti \(A\) e \(B\) tali che \(A\) contiene \(C\) e \(B\) contiene \(D\).

                          
       
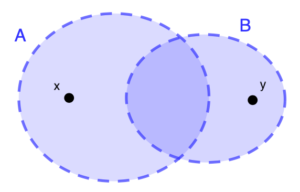
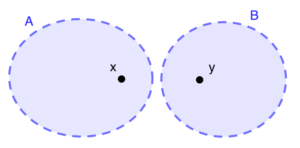
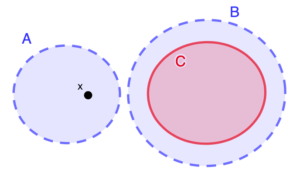
In alto a sinistra, una rappresentazione della condizione degli spazi \(T_1\), in alto a destra quella degli spazi \(T_2\).
In basso a sinistra, quella degli spazi \(T_3\) e in basso a destra degli spazi \(T_4\).

Queste ultime 4 proprietà topologiche vengono spesso dette “assiomi di separazione”. Si dimostra che se uno spazio è \(T_4\) allora è anche \(T_3\), e se è \(T_3\) allora è anche \(T_2\), e se è \(T_2\) allora è anche \(T_1\). Vedetela così, negli spazi \(T_1\) abbiamo un numero di aperti appena sufficiente a distinguere i vari punti, negli spazi \(T_2\) questa distinzione è ancora più precisa -riusciamo a separare gli aperti e i punti-, fino ad arrivare agli spazi \(T_4\) dove abbiamo così tanti aperti e così precisi da poter non solo separare i punti, ma anche gli insiemi chiusi. Gli spazi \(T_1\) sono i più semplici, i meno ricchi, mentre gli spazi \(T_4\) sono i più articolati e quindi quelli in cui si riescono a trovare risultati più potenti. Nella pratica gli spazi più utilizzati sono gli spazi \(T_2\): sono più generali degli spazi \(T_4\), richiediamo meno cose, ma hanno quel tanto in più degli spazi \(T_1\) che basta per ottenere risultati molto interessanti.

È ora di concludere. Le proprietà topologiche sono veramente una sorta di identikit degli spazi topologici, ci dicono quali sono le loro caratteristiche fondamentali e ci aiutano a distinguere spazi che non possono essere omeomorfi. Sono uno strumento estremamente utile e, a suo modo, semplice, ma non mettono fine alla storia. Ci sono molte domande a cui le proprietà topologiche (comprese quelle che non vi ho mostrato) non riescono a rispondere, e per farlo dovremo introdurre un nuovo concetto, quello di omotopia. Ma perché rovinarvi la sorpresa, parleremo di queste cose nella prossima puntata!

5 – continua