Nicola Ciccoli ci presenta il suo diario di bordo di questi mesi di didattica universitaria a distanza. Un racconto appassionante di come si possa ripensare la propria professione. Questa è la quinta puntata. Tutte le puntate le troverete a mano a mano a questo link.
Applicazioni
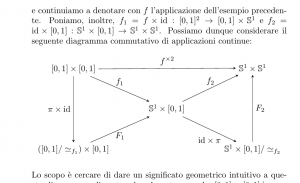
Il diagramma “a farfalla” nei miei appunti.
Una delle cose che personalmente più amo di questo corso è il fatto che molti dei concetti matematici di cui si parla sono cose che si possono visualizzare sotto i nostri occhi tutti i giorni. Questo richiede, però, come dicevo prima una attivazione dello sguardo resa possibile da un primo riconoscimento guidato. Per questo nel corso, ogni tanto, inserisco divagazioni tese a sottolineare alcune delle esperienze reali in cui la geometria differenziale trova applicazione. Divagazioni a contenuto matematico hanno riguardato la curva della palla da tennis, il modo in cui si mangia la pizza e il modo in cui si sbuccia un arancia. Le reazioni registrate sul diario di bordo mi sembra confermino il fatto che sul rapporto tra matematica astratta e realtà pratica ci sia molto da lavorare, ancora.
- Irene: Questa prima settimana di lezione è stata molto interessante, nonostante la mia “paura” per questa disciplina, ho apprezzato molto il fatto di iniziare ad applicare concetti tipo gli omeomorfismi che prima vedevo solo come astratti.
- Davide: In particolare ho trovato affascinante l’applicazione di questo risultato all’esempio piano-sfera riferito al fatto che è effettivamente impossibile creare una cartina geografica effettivamente precisa.
- Stefania: Il fatto che esista una soluzione matematica per tenere inclinato lo spicchio di pizza in modo tale da non far cadere il condimento mi meraviglia. È come se mi desse la conferma che non sto studiando qualcosa di veramente astratto, ma qualcosa che al contrario è alla base di ogni aspetto della vita.
- Marcella: Molte volte mi chiedo: attorno a me dove è tutto ciò che studio. Poi arrivo a lezione e la prima immagine che il prof condivide è quella di una palla da tennis. Allora non mi resta che riflettere su quanto di ciò che studio è intorno a me. Forse è vero, è tutta una questione di attenzione. e anche chi avrebbe mai pensato che attorno a una semplicissima arancia ci fosse tanta geometria… oppure Oltre alle spiegazioni puramente geometriche e matematiche è sempre interessante ascoltare curiosità, se così posso definirle, riguardanti esempi pratici appartenenti alla vita reale.
- Teresa: Mi piace vedere come la matematica si leghi anche ad altre discipline o al quotidiano. Soprattutto mi piace vedere qual è la teoria matematica che si nasconde dietro le cose. E’ un aspetto che mi son resa conto di approfondire poco. Spero di rimediare.
- Luigi: Mi piace molto che in ogni argomento affrontato vediamo esempi quotidiani e reali che fanno comprendere in modo più semplice e divertente le cose studiate. Il potere e la bellezza della matematica.
- Giorgia: Spesso mi chiedevo a cosa servissero alcune materia e quale fosse la loro utilità nella vita reale, ma solo ora capisco che ogni cosa ha una forma e proprietà mai dovute al caso.
- Rossella: Quando abbiamo fatto la lezione in cui abbiamo affrontato l’argomento pizza, ho trovato molto stimolante il fatto che ogni aspetto della nostra vita, anche il più inaspettato e banale, in realtà sia profondamente legato alla matematica; è bello vedere come in realtà, una materia così tanto odiata com’è la matematica, sia un mondo così bello e aperto a ogni tematica. È stato interessante vedere anche questo aspetto a lezione, perché stimola ancora di più lo studio.
Una riflessione mi sembra necessaria. Preoccupati dalle tante situazioni in cui seguire l’intuizione senza saperla affiancare con una analisi rigorosa induce in errore, finiamo (a volte) per convincere alcuni nostri studenti che l’intuizione è un male assoluto e che la matematica inizia e finisce nelle formule che scriviamo. Con il risultato che disegnare sembra essere una eresia, riconoscere in un oggetto reale un concetto astratto una novità e che il campo d’applicazione della matematica sembra essere sempre e solo autoriferito. Sappiamo bene che non è così eppure spesso sembra che la preoccupazione principale dei nostri insegnamenti sia crescere gli studenti di matematica in una visione della loro disciplina asettica e distante. Intendiamoci, chi scrive sa bene quanti danni può fare

Qual è l’equazione della cucitura di una palla da tennis? E come mai è proprio quella? Risponde a delle necessità pratiche di qualche tipo?
una intuizione matematica interamente priva di rigore, quanto sia necessario lavorare per fare interiorizzare un giusto livello di precisione di ragionamento e di linguaggio ai ragazzi che escono dalle scuole superiori. Semplicemente mi chiedo se non dovremmo avviare una riflessione un po’ più approfondita, dotata appunto di mezzi più rigorosi e scientifici che non la semplice ispirazione del singolo docente, su dove e come si debba trovare la giusta via nell’insegnamento tra intuizione e rigore, tra astrazione e realtà. Non penso che questo equilibrio si trovi facilmente affidandolo puramente al caso; temo che troppo spesso le nostre lezioni facciano propria la famosa frase dell’abate Amaury: “sterminateli tutti, Dio [il Dio dei matematici] saprà riconoscere i suoi.
Le lezioni e gli strumenti tecnici
Lavagna o slides? Whiteboard elettronica o appunti? Ci ho riflettuto per mesi senza sapermi decidere. E quale ruolo dare alla possibilità, improvvisamente, di inserire nella lezione con un clic una animazione presa da Geogebra, una immagine scaricata da Internet, una Gif preparata da me, un video di Youtube? Credo di aver veramente provato di tutto. Ho mostrato come varia la forma di una famiglia parametrica di curve al variare di un parametro usando Mathematica online e ho fatto uno studio di grafico di funzione sulla mia lavagna nera artigianale. Che impressione ne hanno ricavato gli studenti?
Anzitutto ho avuto conferma di una mia idea. Il ritmo ottimale di una lezione si ha scrivendo in diretta: lavagna o whiteboard che sia, visto che le slides tendono a produrre lezioni troppo veloci. In questo gli studenti sono stati sostanzialmente unanimi:
- Martina: Le lezioni di questo corso sono online e il professore usa le sue dispense, quest’ultimo non scrive alla lavagna come sono sempre state le lezioni fino a prima della pandemia e quindi, di conseguenza, nello spiegare ha una velocità maggiore che a volte può disperdere.
- Maurizio: Preferisco quando fa le lezioni con le lavagne piuttosto che con le slide perché mi risultano più chiari i concetti andando leggermente più piano, mentre con le slide risulta più difficile seguire.
- Teresa: Devo dire però, che mi sono trovata in difficoltà nel seguire passo passo le lezioni, in quanto la spiegazione con le dispense del professore diventa ovviamente più veloce, quindi spesso ho scritto solo degli accenni di argomenti o teoremi.
- Irene: Gli argomenti nelle ultime lezioni si sono fatti più complicati ma l’utilizzo della lavagna elettronica se può sembrare che rallenti i tempi di spiegazione, permette di seguire meglio e con più calma. Questo infatti, permette di non scrivere pedissequamente cose su un foglio ma dà la possibilità anche di capire e annotare cose che vengono dette dal professore per rendere la spiegazione più esaustiva.
- Giorgia: Non sono riuscita a seguire tutte le lezioni questa settimana ma ho apprezzato il metodo di lezione con la lavagna online, riesco ad essere molto più concentrata delle lezioni fatte seguendo il pdf già scritto.
- Luigi: Infatti, diversamente da quello che ho sentito da molti miei compagni [questa indicazione indiretta è l’unica a favore delle lezioni con le slide: tendo a leggerla più come una indicazione della importanza di avere le slide a disposizione], io trovo di gran lunga più produttivo ed efficace svolgere lezioni sulla lavagnetta, non solo perché la velocità è ridotta (e di conseguenza riesco anche a riflettere con più calma su quello che scrivo) ma anche perché credo sia molto istruttivo il mostrarci come viene scritta una determinata cosa: con quale ordine i concetti vengono spiegati e dove magari vengono fuori più errori/sviste, aiutandomi ad aggiustare il tiro per una possibile futura esposizione da parte mia.
Nessuno ha menzionato differenze tra la scrittura a mano e la possibilità, che ho usato spesso, di scrivere direttamente in TeX; una procedura che a me sembrava troppo laboriosa (non potendo fare uso di nessuna macro) ma che loro non sembrano aver sofferto troppo (è anzi possibile che qualcuno abbia imparato qualche comando Latex). In generale la varietà di strumenti di utilizzati in qualche caso è stata percepita come stancante (anche dal docente) ma in generale ho avuto l’impressione che gli studenti si siano sentiti più giustificati nello sperimentare loro stessi l’utilizzo delle risorse disponibili online.
Veniamo, ora, a una analisi delle altre prove di esonero e del modo in cui sono state recepite dagli studenti.
E1: esercizi
Lo studio delle proprietà dei planisferi è stato uno dei motori storici dello studio della geometria delle superfici, come risulta chiaramente dalla lettura dei lavori di Eulero sulla curvatura.
Gli esercizi proposti, come detto, sono stati non tipici, non riducibili a una semplice tipologia di calcolo, ma piuttosto l’occasione per cercare di stimolare una riflessione personale. Anche nella correzione ho messo molta attenzione sulla completezza degli argomenti, oltre che sulla loro correttezza, invitando tutti a mettere in discussione anche le convinzioni di base, sui cui a volte si annidando delle misconcezioni foriere di errore. Complessivamente l’impressione ricevuta è che gli studenti che hanno partecipato all’esonero abbiano apprezzato il fatto di essere un po’ guidati nel ritmo di studio, spinti com’erano a studiare settimana per settimana e non solo in prossimità dell’esame. Hanno inoltre certamente apprezzato il tempo a disposizione per riflettere un po’ più a lungo sui problemi proposti e di potersi svincolare dalle tempistiche strette degli esercizi in presenza. Gli esercizi sono spesso stati percepiti come difficili rispetto al solito e i ragazzi hanno avuto l’impressione di doversi confrontare con un maggiore livello di frustrazione per il fatto di non vedere immediatamente la strada per la soluzione. La cosa era voluta e lo scopo era esattamente quello di stimolare le loro capacità di reazione a questo tipo di difficoltà.
- Stefania: Domenica ho consegnato il terzo esonero; in altre materie, nessun professore utilizza questo metodo ma confermo di trovarlo altamente producente perché mi aiuta a mantenere un contatto continuo e costante con la materia, come ho già detto nello scorso diario e inoltre mi aiuta a collaborare positivamente con i miei compagni, mi è successo che dopo aver fatto numerosi tentativi per dimostrare un punto di un esercizio non andati a buon fine, mi sono confrontata con un ragazzo e in due abbiamo unito i ragionamenti e siamo arrivati velocemente alla soluzione.
- Irene: Gli esercizi di esonero sono stati una grande opportunità per me, poiché mi hanno dato la possibilità di riflettere su un problema per un tempo maggiore rispetto ad un classico esame scritto. Devo dire che sono stati frustranti, perché a volte non riuscivo subito ad ottenere quello che avrei voluto, o pensavo a procedimenti che non mi convincevano del tutto, e quindi mi lasciavano con il dubbio sulla loro correttezza o meno.
- Luigi: Mi spiego meglio: non avendo quella “fretta” di completare il tutto entra in gioco un ragionamento molto più dettagliato, reso possibile principalmente grazie all’impiego di un tempo molto maggiore rispetto a quello di un esonero “standard”. Questo mi ha permesso di osservare il problema da diversi punti di vista, dandomi la possibilità di provare strade di risoluzione diverse e scegliere poi la migliore; sono insomma certo che questi esercizi non apparterranno alla categoria di quelli di cui ci si dimentica il giorno dopo averli risolti.
- Marcella: Gli esercizi riescono a farmi avvicinare alla materia in maniera più concreta rispetto alla teoria.
- Martina: Gli esercizi ci hanno “obbligati” a rimanere sempre a contatto della materia, a metterci alla prova e a riflettere più tempo anche su quello che non è immediato.
E3: progetto
Ho messo a disposizione degli studenti circa dieci casi di studio: cinque domande teoriche sulle curve e cinque famiglie di curve che potevano essere studiate, invitandoli a scegliere una di queste domande e approfondirla in tutti i modi possibili (calcoli, storia, applicazioni) e di svolgere questo compito a scelta: da soli oppure in gruppo con il vincolo che il gruppo non potesse comprendere più di tre studenti. La ragione del limite era avere gruppi piccoli nei quali, abitualmente, è difficile che non ci sia almeno una parte di contributo per ognuno. Non volendo però forzare scelte possibilmente onerose sul piano organizzativo o sul piano emotivo, data la situazione, la possibilità di fare il compito individualmente è rimasta aperta. Infatti si sono formati alcuni gruppi e ci sono state alcune consegne individuali.
Purtroppo, sul piano tecnico, non sono riuscito a individuare il metodo più efficace per garantire che ognuno scegliesse solo uno dei progetti.
Il risultato è stato che tutti hanno scelto i casi di studio di curve esplicite e vari progetti si sono sovrapposti nel contenuto. Due gruppi mi hanno chiesto di cambiare progetto, dopo la scelta, per via di grosse difficoltà con i calcoli (che in qualche caso erano veramente un po’ onerosi). Ho, in entrambi i casi, invitato ad insistere e non scoraggiarsi e accontentarsi, eventualmente, anche di risultati parziali. Un gruppo ha accolto questo suggerimento, un altro ha comunque preferito modificare il progetto.
Su questa sezione non ho commenti diretti da parte degli studenti essendo la consegna slittata a dopo la fine delle lezioni (anche per evitare sovrapposizioni di scadenze con gli esoneri degli altri corsi). Inoltre il piano originale di fare un incontro di controllo a metà strada con ciascun gruppo/singolo si è rivelato sostanzialmente impossibile per motivi di tempo e questo ha reso sostanzialmente impossibile l’idea di una verifica formativa in corso d’opera. Dovessi ripetere una esperienza del genere la pianificherei meglio sul piano della tempistica: il controllo in corso dovrebbe essere reso possibile e introdurrei degli incentivi per il lavoro su questioni più teoriche.
I risultati sono stati comunque interessanti e tutti i partecipanti hanno portato a termine questi progetti positivamente. In qualche caso era evidente che la richiesta di informazioni di contesto, storiche e applicative, è stata risolta con una breve ricerca online e il contenuto è stato un copia e incolla dei primi siti disponibili. Credo che per richiedere un lavoro più approfondito in questa direzione il lavoro di progetto dovrebbe essere preparato, anche dal lato del docente, molto meglio. Ma credo che la cosa porterebbe un po’ troppo lontano dagli obiettivi specifici di questo corso: non è previsto che durante Geometria IV imparino a lavorare sulle fonti d’informazione, sull’approfondimento, sulle notizie storiche. Mi era sufficiente che prendessero coscienza del fatto che ciascuna delle curve inserite nei progetti ha alle spalle motivazioni e studi: questo obiettivo minimale penso di averlo ottenuto.















