Chissà che cosa avrebbe pensato Bertie Charles Forbes se avesse saputo che la rivista di economia da lui fondata nel 1917 avrebbe ospitato sulle sue pagine un articolo che ha come oggetto una teoria matematica di notevole astrattezza quale la teoria delle categorie? Di questo e di altro ci parla Giuseppe Metere.
Che ci sia un rapporto stretto tra la matematica e le scienze economiche è cosa nota, dal Tractatus di Luca Pacioli sulla partita doppia del 1494, agli studi più recenti di teoria dei giochi, delle decisioni, del comportamento dei mercati finanziari. Tuttavia, la Teoria delle Categorie è considerata spesso molto astratta persino dai matematici stessi – o almeno da alcuni. Perché dovrebbe interessare il lettore della versione online di Forbes?
Una possibile risposta la si può leggere nell’articolo di Jayshree Pandya “The future will be formulated using category theory” (Forbes.com, luglio 2019 [1 ]https://www.forbes.com/sites/cognitiveworld/2019/07/29/the-future-will-be-formulated-using-category-theory/#6cefafc9625e ) ossia “Il futuro sarà formulato utilizzando la teoria delle categorie”. Secondo l’autrice, l’attuale sviluppo della conoscenza scientifica potrebbe non essere in grado di spiegare completamente la vita umana, il pensiero, la coscienza, e neanche la natura e l’origine della materia, dell’universo. Questo perché, per molto tempo, chi si occupa di scienza è stato abituato a considerare i fenomeni fisici all’interno di sistemi chiusi. I sistemi complessi, invece, come ad esempio l’ecosistema umano, sono costituiti da diversi sistemi, alcuni chiusi, ma altri aperti, comunque tutti interconnessi tra loro.
L’idea è quella di spostare il focus dall’analisi dei singoli componenti di un sistema, allo studio delle relazioni tra diversi sottosistemi. L’obiettivo è applicare questo paradigma alla progettazione di sistemi complessi in ambiti diversi, oltre l’ecosistema umano, che l’autrice definisce con l’acronimo CAGS (Cyberspace, Aquaspace, Geospace, Space: i luoghi contesi sui quali nessuno stato esercita il controllo completo, e per i quali è necessario impegnarsi per gestirli al meglio per il futuro dell’umanità, vedi [2 ]https://www.forbes.com/sites/cognitiveworld/2019/05/01/the-coming-clash-of-the-contested-commons/).
Galileo, nel Saggiatore, affermava che il libro della natura “è scritto in lingua matematica”; seguendo la sua intuizione, su quale idioma matematico possiamo basare la comprensione dei sistemi complessi contemporanei? In fondo, la matematica si è sempre evoluta insieme all’uomo, spesso riflettendo e riflettendosi nella storia dell’umanità. Quale matematica, allora per il nostro mondo, o meglio, per la consapevolezza che abbiamo di esso? Serve una matematica che sia focalizzata sulle relazioni tra le cose, più che sullo studio delle cose in sé. Per rispondere a questa domanda, l’autrice si affida alle parole del fisico matematico John C. Baez, secondo cui la teoria delle categorie potrebbe essere lo strumento adatto per comprendere la realtà relazionale in cui viviamo.
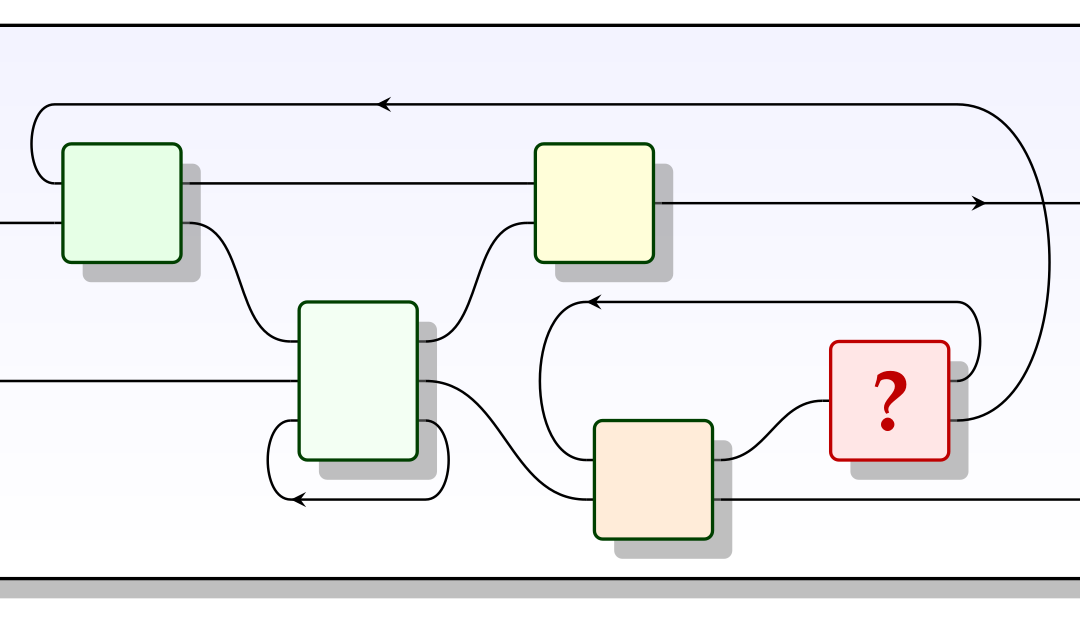
La teoria delle categorie nasce nel 1945 dal lavoro di Samuel Eilenberg e Saunders Mac Lane sul rapporto tra spazi e loro invarianti omotopici e omologici [3 ]S. Eilenberg and S. Mac Lane, General theory of natural equivalences, Trans. Amer. Math. Soc., Vol 58, No. 2 (1945). Sebbene si sia originata in un ambito così specifico, la teoria ha un carattere generale che negli anni successivi ha prodotto notevoli cambiamenti non solo nella topologia algebrica, ma anche in altre discipline matematiche, come ad esempio in geometria algebrica, logica matematica, combinatoria, teoria dei fondamenti, informatica.
Un’idea centrale dell’approccio categoriale è che si possano studiare le proprietà di un oggetto matematico (spazio topologico, gruppo, spazio vettoriale, campo, anello etc.) osservando le relazioni tra esso e gli altri oggetti che lo circondano. Applicato allo studio dei sistemi complessi, questo punto di vista ci porta a una diversa comprensione dei fenomeni (in antitesi al classico approccio riduzionista).
Sebbene un sistema possa essere scomposto in parti più semplici, non si può, in generale, ridurre lo studio dell’intero sistema allo studio delle sue parti, ma è necessario osservare in che modo le singole parti interagiscono fra loro. La teoria delle categorie offre la possibilità di farlo dal punto di vista formale, indagando i modi, i pattern, l’algebra delle relazioni tra oggetti.
Per questo, conclude l’articolo, “la teoria delle categorie sta diventando rapidamente importante per la comprensione dei problemi che l’umanità sta affrontando o si troverà ad affrontare”, auspicando che la si possa applicare “alla definizione e alla progettazione di sistemi a tutti i livelli, considerando sempre le relazioni di interconnessione tra unità individuali discrete allo scopo di costruire il nostro futuro collettivo”.
Pur senza sposare l’enfasi di Jayshree Pandya, è innegabile che la teoria delle categorie stia suscitando un certo interesse in diversi ambienti della comunità scientifica internazionale. Le ultime due conferenze, “Category Theory 2019” e “Applied Category Theory” svoltesi rispettivamente a Edimburgo e a Oxford a luglio di quest’anno, hanno registrato un vero e proprio boom di partecipazione. Le ragioni di questo interesse sono molteplici. Probabilmente una di esse è che essa riesce a offrire allo stesso tempo sia un contesto concettuale che un ambiente di calcolo in cui inquadrare problemi ed elaborare strategie. D’altro canto, la teoria delle categorie è una teoria matematica, con le sue definizioni e i suoi teoremi, che in oltre settannt’anni di studio e ricerca si è via via consolidata come corpus di conoscenze e come pratica di lavoro. E’ certamente una disciplina relativamente giovane, ma, per usare le parole di F. William Lawvere, “concentra le caratteristiche essenziali di secoli di esperienza matematica” [4 ]An interview with F. William Lawvere, Bull. Int. Center for Math., Coimbra (2007).
A questo proposito riteniamo utile ricordare la prossima conferenza internazionale “Category Theory 2020” si terrà in Italia, a Genova, durante il mese di giugno del prossimo anno.
Giuseppe Metere
Professore Associato di Algebra
Dipartimento di Matematica e Informatica
Università degli Studi di Palermo
Approfondimenti
Per una introduzione amichevole alla teoria delle categorie si può consultare il libro di Tom Leinster [5 ]T. Leinster, Basic category theory, Cambridge University Press (2014) (liberamente scaricabile), mentre i testi di riferimento classici sono S. Mac Lane [6 ]S. Mac Lane, Categories for the working mathematician, Springer (1971) e l’enciclopedico testo di Borceaux [7 ]F. Borceux, Handbook of categorical algebra, Cambridge University Press (2009).
Per un punto di vista recente sulle applicazioni della teoria delle categorie alle scienze in genere, un buon punto di partenza è certamente la raccolta delle lezioni tenute al M.I.T. da David Spivak e Brendan Fong nel 2018 [8 ]D. Spivak and B. Fong, An invitation to applied category theory: seven sketches in compositionality, Cambridge University Press (2019) (anche queste liberamente scaricabili).
Note e riferimenti
| ⇧1 | https://www.forbes.com/sites/cognitiveworld/2019/07/29/the-future-will-be-formulated-using-category-theory/#6cefafc9625e |
|---|---|
| ⇧2 | https://www.forbes.com/sites/cognitiveworld/2019/05/01/the-coming-clash-of-the-contested-commons/ |
| ⇧3 | S. Eilenberg and S. Mac Lane, General theory of natural equivalences, Trans. Amer. Math. Soc., Vol 58, No. 2 (1945) |
| ⇧4 | An interview with F. William Lawvere, Bull. Int. Center for Math., Coimbra (2007) |
| ⇧5 | T. Leinster, Basic category theory, Cambridge University Press (2014) |
| ⇧6 | S. Mac Lane, Categories for the working mathematician, Springer (1971) |
| ⇧7 | F. Borceux, Handbook of categorical algebra, Cambridge University Press (2009) |
| ⇧8 | D. Spivak and B. Fong, An invitation to applied category theory: seven sketches in compositionality, Cambridge University Press (2019) |