La congettura di Goldbach, spiegata da Bruno Martin, docente presso il Laboratorio di ricerca in Matematica dell’Université du Littoral, Côte d’Opale, per Images des Mathématiques. Traduzione di Elena Toscano.
Traduzione dell’articolo di Bruno Martin, «La conjecture de Goldbach»— Images des Mathématiques, CNRS, 2013. (link articolo originale: http://images.math.cnrs.fr/La-conjecture-de-Goldbach-1473.html)
La congettura di Goldbach
Bruno Martin
Docente presso il Laboratorio di ricerca in Matematica dell’Université du Littoral, Côte d’Opale
(page web: http://www-lmpa.univ-littoral.fr/~martin/)
Che strana idea sommare dei numeri primi! Eppure è ciò che ha fatto un tale Goldbach più di 250 anni fa…
In questo articolo esploreremo una delle più famose congetture matematiche. Tale congettura è stata formulata nel 1742 dal matematico tedesco Christian Goldbach in una lettera (riprodotta qui sotto) indirizzata al matematico svizzero Leonhard Euler [1]. Si tratta di uno dei più antichi problemi matematici a oggi irrisolti.
La congettura di Goldbach riguarda i numeri primi. Piuttosto che enunciarla immediatamente, inizieremo con l’introdurre l’insieme dei numeri primi, dare la sua proprietà fondamentale e vedere le ragioni che possono portare a enunciare la congettura di Goldbach.
In tutto l’articolo, si prenderanno in considerazione numeri interi maggiori o uguali a 1, vale a dire i numeri 1, 2, 3, …. Inoltre, quando diremo che un numero è maggiore di un altro, tale affermazione è da prendere in senso ampio, vale a dire che questi numeri possono eventualmente essere maggiori o uguali.
I numeri primi
Si dice che un numero è primo se è divisibile solo per 1 e per se stesso, ed è maggiore di 1 [2]. Il numero 1 non è dunque primo. I numeri 2 e 3 sono primi, essi sono divisibili solo per se stessi e per 1. Viceversa, il numero 4 non è primo perché è divisibile per 2. Infatti, se si conoscono le sue tavole di moltiplicazione, è facile iniziare un elenco di numeri primi:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53 …
Questo elenco si ferma? Ne riparleremo dopo.
Il seguente risultato giustifica, da solo, l’interesse per i numeri primi.
Teorema: Ogni numero intero maggiore o uguale a 2 o è un numero primo o si può esprimere come prodotto di numeri primi.
In altre parole, eseguendo delle moltiplicazioni tra numeri primi si possono ritrovare tutti gli altri numeri. Verifichiamolo con un esempio: prendiamo il numero 60. Non è primo poiché è divisibile per 10. Si ha infatti:
Ma né 6 né 10 sono numeri primi. Infatti, 6 è divisibile per 3 e 10 è divisibile per 5. Più precisamente:
6 = 2 × 3 e 10 = 5 × 2.
Possiamo dunque scrivere:
60 = 6 × 10 = (2 × 3) × (5 × 2) = 2 × 3 × 5 × 2.
E qui ci si ferma perché 2, 3 e 5 sono numeri primi [3]. In effetti non è molto difficile ispirarsi a tale esempio per dimostrare il teorema.
Abbiamo visto che, moltiplicando tra loro numeri primi, si possono ritrovare tutti i numeri maggiori o uguali a 2. Accade lo stesso fenomeno sommando tra loro numeri primi? In altre parole, possiamo ritrovare tutti i numeri più grandi di 2 effettuando solo delle addizioni tra numeri primi?
Una veloce riflessione mostra che la risposta a questa domanda è molto semplice. Infatti, sommando il numero 2 a se stesso tutte le volte che è necessario, si possono ottenere tutti i numeri pari. E se un numero è dispari, è sufficiente sottrargli 3: si ottiene quindi un numero pari che, a sua volta, si ottiene sommando dei 2. Per esempio, prendiamo il numero 29, sottraiamogli 3 e otteniamo 26. E 26 è ottenuto sommando tredici volte il numero 2 a se stesso. Si ha dunque 29 = 3 + 13 × 2 = 3 + 2 + 2 + … + 2. Con un simile procedimento, più il numero è grande maggiore è il numero di addizioni da effettuare. Che cosa accade se si limita il numero di addizioni?
Domanda: È possibile ottenere un qualunque numero maggiore di 2 sommando solo dei numeri primi e senza mai superare un numero fissato di addizioni?
Per esempio, è possibile trovare un qualsiasi numero limitandosi a effettuare venti addizioni tra numeri primi? Questa volta, la risposta a questa domanda è tutt’altro che banale.
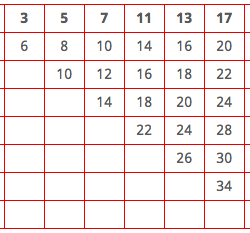
Iniziamo a vedere che cosa succede quando si sommano solo due numeri primi. Per il momento ignoriamo il numero 2 e calcoliamo tutte le possibili somme con i numeri primi compresi tra 3 e 19. Per far ciò disponiamo i numeri primi sulla prima riga e sulla prima colonna di una tabella a doppia entrata
e riempiamo la tabella nel modo seguente: in ogni cella mettiamo la somma dei due numeri primi che indicizzano la cella. Cominciamo:
Non è necessario riempire le altre caselle perché i risultati saranno esattamente gli stessi già ottenuti nella parte superiore della tabella.
Prima constatazione: tutte le somme ottenute sono numeri pari. È sorprendente? No, perché un numero primo maggiore o uguale a 3 è sempre dispari. Infatti, se fosse pari, sarebbe divisibile per 2 e non sarebbe primo; e quando si sommano tra loro due numeri dispari il risultato è sempre un numero pari.
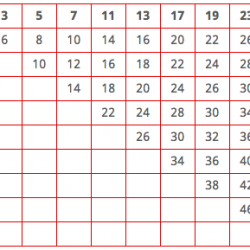
Inoltre, il più grande numero pari ottenuto è 38 e si può constatare che tutti i numeri pari compresi tra 6 e 38 sono presenti nella tabella. Questo fenomeno persiste? Per scoprirlo, continuiamo un po’ i nostri calcoli sommando tutti i numeri primi compresi tra 3 e 29. Per farlo è sufficiente aggiungere due righe e due colonne alla nostra tabella iniziale:
e quindi completare le celle mancanti:
Il più grande numero pari ottenuto è 58. Si ottengono quasi tutti i numeri pari compresi tra 6 e 58, ma non tutti: 44, 50, 54 e 56 mancano all’appello. Ma essi appariranno non appena si aggiungeranno le righe e le colonne corrispondenti ai due numeri primi seguenti, 31 e 37, dal momento che 44 = 31 +13, 50 = 31 + 19, 54 = 31 +23 e 56 = 37 + 29.
Questi calcoli dunque ci portano naturalmente a immaginare che, se continuiamo a estendere questa tabella aggiungendo dei numeri primi, otterremo progressivamente tutti i numeri pari maggiori di 6. In altre parole ogni numero pari maggiore di 6 potrebbe essere ottenuto sommando tra loro due numeri primi. Notiamo che il 4 è la somma di due numeri primi dato che 4 = 2 + 2. Così sembra che l’addizione di due numeri primi sia sufficiente per ottenere qualsiasi numero pari maggiore di 4.
Possiamo fare la stessa cosa per i numeri dispari? Per ottenere un numero dispari mediante un’addizione è necessario sommare tra loro un numero pari e un numero dispari. L’unico numero primo pari è il 2 e finora l’avevamo messo da parte. Sommandolo ai numeri primi dispari si riesce a ottenere tutti i numeri dispari? Ciò significherebbe dire che ogni numero dispari è immediatamente preceduto da un numero dispari che è un numero primo, il che è falso come si può facilmente constatare nel caso di 11 (il numero dispari che lo precede, 9, non è primo). Insomma non si può sperare di ritrovare tutti i numeri limitandosi a sommare tra loro due numeri primi.
Partiamo dall’ipotesi che ogni numero pari maggiore o uguale a 4 sia in realtà la somma di due numeri primi. È facile vedere che un numero dispari maggiore o uguale a 7 è sempre uguale alla somma di tre numeri primi. Infatti, se gli sottraiamo 3, si ottiene un numero pari maggiore o uguale a 4, che è dunque la somma di due primi in virtù della nostra ipotesi. Sommando questi due numeri primi e il numero 3 si ritorna al numero di partenza che è dunque la somma di tre numeri primi.
Si noti che 2, 3 e 5 sono già numeri primi e quindi nessuna addizione tra numeri primi è necessaria per ottenerli. Sembra dunque che qualsiasi numero maggiore o uguale a 2 o sia primo o sia la somma di due o tre numeri primi, cosa che riassumiamo dicendo che ogni numero intero è la somma al più di tre numeri primi. Con alcune piccole differenze, questa è esattamente la congettura che Goldbach ha formulato nella sua lettera a Eulero. Ma in generale noi assimiliamo la congettura di Goldbach all’ipotesi fatta sopra sui numeri pari, che è stata enunciata da Eulero nella sua risposta a Goldbach.
Congettura (Goldbach-Eulero, 1742): Qualsiasi numero pari maggiore o uguale a 4 è la somma di due numeri primi.
Nel seguito, se non diversamente specificato, quando diremo “congettura di Goldbach” è a tale enunciato che faremo riferimento.
Come abbiamo visto, la congettura Goldbach implica che qualsiasi numero maggiore di 2 è la somma al più di tre numeri primi. Si osserva quindi un fenomeno sorprendente. Se da un lato i numeri primi sono principalmente conosciuti per la loro capacità di generare tutti gli altri numeri mediante moltiplicazioni, dall’altro sembra possibile fare lo stesso mediante delle addizioni, e non più di due. Ma ricordiamo che in questa fase nulla è stato ancora dimostrato: non siamo ancora in grado di fornire una risposta affidabile alla nostra domanda iniziale, vale a dire, possiamo ottenere tutti i numeri effettuando un numero limitato di addizioni tra numeri primi?
Torneremo su tale questione più avanti. Per ora ci concentreremo per un attimo sulla congettura di Goldbach e tenteremo di fare luce.
La congettura di Goldbach è vera?
Vi sono due possibili risposte a questa domanda. O non lo è e questo significa che esiste almeno un numero pari che non è la somma di due numeri primi, ossia esiste un contro-esempio. Per trovarlo, si può scrivere un codice al computer per determinare se un dato numero pari è la somma di due numeri primi e utilizzarlo per testare molti numeri pari. Finora questo metodo non ha fornito alcun contro-esempio: ad oggi è stato verificato che ogni numero pari inferiore a 4 × 1018 è la somma di due numeri primi [4]. Se un contro-esempio esiste, è un numero enorme!
C’è dunque chi si dichiara fortemente a favore di una risposta affermativa: la congettura di Goldbach è senza dubbio vera. Ma in questo caso è necessario darne una dimostrazione e finora nessuno è riuscito a darla. La congettura di Goldbach, così come il “Problema 3n + 1” (noto anche come “congettura di Collatz”, NdT), è un problema che, nonostante il suo enunciato elementare, rimane attualmente irrisolto.
Tuttavia, tentiamo coraggiosamente la nostra fortuna ragionando sulla nostra tabella estensibile, e iniziamo facendo l’avvocato del diavolo cercando brevemente di confutare questa congettura!
Cerchiamo di dimostrare che la congettura di Goldbach è falsa
Abbiamo iniziato a fare un elenco di numeri primi. Che cosa accadrebbe se fosse finito? Per fissare le idee, supponiamo che ci siano un milione di numeri primi e non di più. La congettura di Goldbach sarebbe semplicemente falsa. Infatti, la nostra tabella sarebbe finita anch’essa. Sarebbe enorme, coinvolgerebbe certamente un numero considerevole di celle, ma non potrebbe mai contenere tutti i numeri pari dal momento che essi sono infiniti! Ma, in realtà, l’elenco dei numeri primi non si ferma. In altre parole, ci sono infiniti numeri primi. E sappiamo dimostrarlo [5].
Va bene, esistono numeri primi grandi quanto si vuole, ma è possibile che essi siano molto rari. Non è facile attribuire un preciso significato al termine raro. Immaginate di camminare lungo un sentiero segnato con pietre miliari numerate da 1 a … infinito e di annotare su un taccuino i numeri primi che incontrate. Siete sicuri di incontrare dei numeri primi man mano che proseguite la vostra marcia. Ma potrebbe accadere che la distanza da percorrere tra un numero primo e il seguente sia in generale via via più lunga. A tal punto che si potrebbe immaginare che la scelta dei numeri primi sia troppo limitata e che non ve ne siano a sufficienza per ottenere tutti i numeri pari. Non diciamo altro per il momento.
Sembra in ogni caso che una buona stima della frequenza dei numeri primi sia un ingrediente importante, se non essenziale, per comprendere la congettura Goldbach.
Proviamo a dimostrare che la congettura di Goldbach è vera… fino a 100
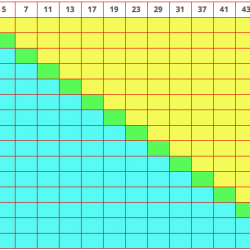
Continuiamo la nostra riflessione cercando questa volta di considerare delle argomentazioni a sostegno della congettura di Goldbach. Ampliando ancora un po’ la nostra tabella ed effettuando le necessarie addizioni, potremo verificare che ogni numero pari compreso tra 4 e 100 è la somma di due numeri primi. Ma cerchiamo di raggiungere tale obiettivo senza calcolare queste somme! Useremo tutti i numeri primi compresi tra 3 e 53 (se ci si ferma a 47 non si avrà alcuna possibilità di ottenere il numero 100) e poi proveremo a ragionare su questa tabella non completamente riempita.
Quante sono le celle colorate in giallo e verde? In altre parole, quanti risultati possiamo ottenere? La tabella completa è costituita da 15 righe e 15 colonne perché ci sono 15 numeri primi compresi tra 3 e 53, allora vi sono 15 × 15 = 225 celle in totale. Ci sono tante celle gialle quante celle blu e la diagonale verde ha 15 caselle. Vi sono dunque (225 – 15) / 2 ovvero 105 caselle gialle. Se aggiungiamo le 15 celle della diagonale, in totale otterremo 120 numeri pari compresi tra 6 e 106 (= 53 + 53). Tutti i numeri pari tra 6 e 106?
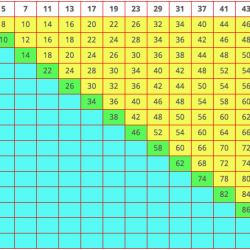
Tra il 6 e 106 (inclusi) vi sono 101 numeri e tra questi 51 sono pari. Le 120 celle sono più che sufficienti per accogliere questi 51 numeri. Ma ricordiamoci delle nostre prime tabelle: alcuni numeri pari sono ottenuti come somma di due numeri primi in modi diversi. Per esempio, il numero 24 è uguale a 17 + 7, 19 + 5 e 13 + 11. Si vede allora che si pone un problema: se alcuni numeri pari “mobilitano” troppi numeri primi, potrebbe accadere che non vi siano numeri primi sufficienti per ottenere tutti gli altri numeri. Nelle nostre precedenti tabelle, nessun numero occupa più di 3 celle, allora supponiamo che il limite di 3 celle per numero rimanga invariato quando la tabella viene ampliata; vale a dire che un numero, qualunque esso sia, non può apparire più di 3 volte nella tabella. Ciò significa che le nostre 120 celle ci permetteranno di ottenere almeno 120/3 = 40 numeri pari distinti. Il nostro tentativo fallisce perché dobbiamo ottenerne 51. Si noti che il nostro ragionamento si basa su due informazioni: il numero dei numeri primi compresi tra 3 e 53 e il numero massimo di celle occupate da un numero pari. Ora confrontiamo le nostre considerazioni con la realtà completando la tabella.
S’impongono due constatazioni:
· La nostra ipotesi di limitare il numero di celle occupate da ogni numero pari a 3 è stata infelice dal momento che alcuni numeri, come il 60, appaiono sei volte.
· Non è stato comunque possibile ottenere tutti i numeri pari inferiori a 106 in questo modo, poiché per esempio 92 (= 31 + 61) non figura nella tabella. La nostra restrizione ai numeri primi inferiori a 53 è stata troppo severa! Abbiamo già incontrato questo fenomeno quando abbiamo preso in considerazione la tabella con i numeri primi compresi tra 3 e 29.
In breve, il nostro ragionamento è fallito e, in ogni caso, non era basato su un’ipotesi valida. Tuttavia esso può essere reso rigoroso e tale che, se si è capaci:
1) di stimare il numero di numeri primi minori di un numero determinato (bisogna essere sicuri che ci siano abbastanza numeri primi);
2) di affermare che il numero di volte che un determinato numero pari appare nella tabella (si dice il numero di rappresentazioni di un intero pari come somma di due primi) non è “troppo alto”,
allora si può dimostrare che una proporzione, diciamo importante, di numeri pari è la somma di due numeri primi, il che è un inizio. Si noti la natura singolare di questa procedura: per dimostrare che ogni numero pari ammette almeno una rappresentazione (è una riformulazione della congettura di Goldbach) si cerca di utilizzare il fatto che non può averne troppe.
In effetti, il punto 1 deriva da un risultato trovato nel 1851 dal matematico russo Pafnuty Chebyshev. L’enunciato è abbastanza tecnico e dice in sostanza che certamente i numeri primi si fanno via via più rari man mano che si avanza sul nostro cammino indicizzato dai numeri, ma comunque non troppo!
Il punto 2 può essere affrontato utilizzando le tecniche note come crivello. Avete forse visto il “crivello di Eratostene” a scuola? Tale tecnica può essere raffinata ed è quello che ha fatto in particolare il matematico norvegese Viggo Brun verso il 1920. Si noti che, di fatto, si crede che il numero di rappresentazioni di un numero pari aumenta in generale all’aumentare della dimensione del numero. Si possono del resto calcolare i numeri di rappresentazioni dei primi numeri pari e rappresentare tali risultati mediante un grafico: si ottiene una nuvola di punti il cui aspetto caratteristico ha suggerito il nome di cometa di Goldbach (vedi immagine sotto, NdT).
La cometa di Goldbach
Si vede per esempio che un numero pari dell’ordine di 1 milione (la notazione 1e+06 significa 1 × 106) ha un numero di rappresentazioni maggiore almeno di 2000. In effetti, si ha anche un’idea abbastanza precisa di quello che dovrebbe essere l’ordine di grandezza teorico del numero di rappresentazioni di un dato numero pari. Ma sia chiaro che si resta allo stadio delle ipotesi.
A questi due ingredienti, il matematico russo Lev Genrikhovich Schnirelmann ne ha aggiunto un terzo – di cui non parleremo qui – che non permette di dimostrare la congettura di Goldbach ma dà, in compenso, una risposta positiva alla nostra domanda iniziale.
Teorema (Schnirelmann, 1930): Esiste un numero N tale che qualsiasi numero maggiore di 2 è la somma al più di N numeri primi.
Schnirelmann dimostra che questo numero N esiste senza darne un valore esplicito. Da allora, molti matematici si sono prodigati per dare dei valori ammissibili per N tanto bassi quanto possibili. Abbiamo visto sopra che non potevamo sperare di prendere N = 2 e ciò che si spera (è la congettura di Goldbach nella sua forma originale) è dimostrare che N = 3 è un valore ammissibile. L’ultimo risultato a oggi riconosciuto è dovuto a Terence Tao (2012) e afferma che possiamo prendere N = 6, migliorando così il precedente record detenuto dal 1995 da Olivier Ramaré con N = 7 [6]. È molto probabile che N = 4 sia ottenuto prossimamente. Siamo così vicini a N = 3, il valore congetturato da Goldbach nella sua lettera? No. Sembra che un abisso ci separi. Come abbiamo già detto, la congettura di Goldbach (nella sua forma originale o in quella dovuta a Eulero) è considerata estremamente difficile e nulla indica che verrà risolta in un futuro prossimo nonostante il duro lavoro di numerosi matematici.
Tutto ciò a che pro?
La congettura di Goldbach, se fosse dimostrata, non costituirebbe probabilmente un risultato molto importante in sé: a differenza di altre congetture matematiche, non ha alcuna influenza diretta su altri problemi e non risponde a una qualche esigenza pratica [7]. Costituirebbe piuttosto la fine di una lunga epopea. Un’epopea tutt’altro che inutile dal momento che ha motivato e motiva ancora lo sviluppo di tecniche matematiche molto raffinate, in particolare la teoria del crivello menzionata sopra, i cui campi di applicazione sono molto vasti. Il fatto che questa congettura abbia resistito così a lungo alle menti più brillanti lascia pensare che nuove idee sono necessarie. Idee che, se dovessero germinare, senza dubbio getterebbero una nuova luce su questi affascinanti numeri primi di cui abbiamo capito ancora troppo poco.
P.S. L’autore ringrazia vivamente Shalom Eliyahu, Christophe Bourel, Cidrolin Barbara Schapira, Boilley Christophe Aline Parreau e Bruno Duchesne per la loro attenta e critica rilettura di questo articolo, così come Jean Fromentin per la sua preziosa assistenza tecnica.
[1] È possibile trovare a questo link http://www.math.dartmouth.edu/~euler/correspondence/letters/OO0765.pdf una trascrizione dattiloscritta della lettera. Per gli amanti del tedesco e del latino!
[2] Senza questa condizione, il numero 1 sarebbe anch’esso un numero primo. Ma alcune considerazioni che non discuteremo qui hanno portato i matematici ad escluderlo. Notare che all’epoca di Goldbach, il numero 1 era considerato primo.
[3] Si potrebbe iniziare scrivendo 60 = 4 × 15 o 60 = 5 × 12 ma alla fine avremmo ottenuto gli stessi numeri primi con lo stesso numero di occorrenze. Si può dimostrare che, più in generale, a parte l’ordine in cui vengono eseguite le moltiplicazioni, vi è un modo per ottenere un determinato numero facendo prodotti di numeri primi.
[4] Tale “verifica” è dovuta al portoghese Tomás Oliveira e Silva (http://www.ieeta.pt/~tos/goldbach.html).
[5] La prima dimostrazione è attribuita a Euclide e la si può facilmente trovare su internet (per esempio:http://it.wikipedia.org/wiki/Teorema_dell%27infinità_dei_numeri_primi, NdT).
[6] Altri risultati parziali sulla congettura di Goldbach si possono trovare sulla pagina di Wikipedia ad essa dedicata.
[7] per quel che ne so io…


















A che punto è il mio commento, inviato nel giugno 2019? Devo ancora attendere o mi devo rivolgere, come mi avete suggerito per il mio commento alla congettura di Collatz, ad una pubblicazine matematica? In questo caso potreste cortesemente indicarmi a quale?
Navigando non sono riuscito a trova la dimostrazione della congettura debole
di Goldbach, ne si trova la dimostrazione dichiarata da Harald Helfott.
Dove posso trovare quella dimostrazione?
Può andare a questo link: https://arxiv.org/abs/1501.05438 L’articolo è accessibile liberamente.
Se tutti i numeri dispari maggiori di 7 possono essere scritti come somma di tre numeri primi significa che uno dei tre addendi deve essere 3;infatti non si potrebbero ottenere i numeri dispari minori di 15; quindi se a tutte le terne di primi che danno i numeri dispari togliamo 3 otteniamo tutti i numeri pari con
la somma di due primi.
La prima frase è falsa. Sarebbe vera se fosse era la congettura di Goldbach forte. Ma allo stato dell’arte, il fatto che un numero dispari maggiore di 7 possa essere scritto come somma di tre numeri primi (dispari), non implica per nulla che uno di questi sia un 3 (altrimenti si otterrebbe appunto la congettura di Goldbach forte da quella debole.
La prima frase è falsa. Sarebbe vera se fosse vera la congettura di Goldbach forte. Ma allo stato dell’arte, il fatto che un numero dispari maggiore di 7 possa essere scritto come somma di tre numeri primi (dispari), non implica per nulla che uno di questi sia un 3 (altrimenti si otterrebbe appunto la congettura di Goldbach forte da quella debole).
Salve,
è stata dimostrata questa congettura?
per riepilogo da wikipedia:
Essa afferma che ogni numero pari maggiore di 2 può essere scritto come somma di due numeri primi (che possono essere anche uguali).
Se sì, dove posso trovarne la dimostrazione, che consultando i motori di ricerca non ho trovato nulla.
Grazie e buona giornata.
Aggiungerei ai commenti precedenti, l’ovvio:
Esistono infinite coppie di numeri pari che sono la somma di 2 numeri primi. E sono tutti quelli che appartengono all’insieme 2n, dove n numero primo, quindi tutti i numeri pari che sono uguali a n+n. Difatti la congettura afferma “…(che possono essere anche uguali)” ed è provato che i numeri primi sono infiniti, ergo…
Beh, si tratta della congettura forte di Goldbach, e no, non è stata dimostrata (ma quella debole sì, che dice che qualsiasi numero dispari maggiore o uguale a 7 può essere scritto come la somma di 3 numeri primi).
L’unico numero pari atipico potrebbe essere 2 ; che si può sempre ottenere come differenza di due numeri primi.
Se ogni numero pari è divisibile per 2 significa che ogni nuimero pari lo possiamo rappresentare come un rettangolo.
Per esempio 28 è rappresentabile dal rettangolo 2 x 14; scrivendo tale rappresentazione come:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 tra i quali i primi: 2,3.5.7,11 e 13
27 26 25 24 23 22 21 20 19 18 17 16 15 14 tra i quali i primi :17,19,23.
Quindi 28 si può ottenere: 5+23; 11+17 .
In questo modo non risulta influente il rerefarsi dei numeri primi perchè la loro quantità consente un numero esuberante di possibilità (vedi precedente intervento).
Esistendo sempre un p greco sia di N che di 2N possimo ottenere qualsivoglia numero pari.
Mancando delle conoscenze per formalizzare queste idee le lascio a chi le sappia utilizzare.
È interessante che in tanti si interessino a questo problema. I professionisti non accettano l’approccio statistico perché non è una dimostrazione in senso stretto. Però esiste la possibilità che la congettura sia vera solo per caso. Per i numeri piccoli è verificata sperimentalmente. Per i grandi è sempre più improbabile trovare un numero per cui non sia vera.
Intorno a 1000 trovare un numero che non si possa esprimere come somma di due numeri primi ha probabilità 10 ^ -10. Per numeri intorno a 1 milione siamo a 10^ -2350 (infatti si trova sperimentalmente che non solo ogni numero è rappresentato da una coppia di numeri primi ma che esistono almeno 4000 coppie per ogni numero)
I numeri primi sono disposti in modo non prevedibile quindi ai fini di questa congettura si possono immaginare disposti casualmente il che vuole dire che una probabilità così bassa equivale ad una certezza ma anche alla certezza che non si possa trovare la dimostrazione.Rassegniamoci e leggiamo il libro lo zio Petros
Un approccio geometrico:
si tratta di un problema di esistenza . La congettura equivale alla ricerca di soluzioni in numeri primi dell’equazione
z=(x+y)/2…. costruire quindi un qualche invariante della varieta’ associata all’equazione che sia un “indicatore” della presenza o meno di numeri primi, e la congettura sarebbe dimostrata (a patto di trascinarla in qualche teoria di equazioni)
Ma se l’ho risolta che devo fare
Scrivi bene la dimostrazione, meglio se in inglese, controlla che tutti i passaggi siano corretti (la congettura di Goldbach è famosa per l’alto numero di dimostrazioni sbagliate) e mandala ad una rivista specializzata https://en.wikipedia.org/wiki/List_of_mathematics_journals
Non sono un matematico, ma un chirurgo in pensione che da qualche anno si diverte coi numeri. La soluzione della congettura mi sembra persino infantile, anche se non saprei tradurla in un algoritmo. Ho 88 anni! Quello che occorre è avere davanti agli occhi la lista dei numeri primi. Scelto un numero primo a caso, parto dal numero pari immediatamente successivo. Dato che i numeri pari finiscono tutti con le cifre 2 – 4 – 6 – 8 – 0, i due numeri primi la cui somma darà il numero pari dovranno finire con le cifre 0 – 1 – 3 – 7 – 9 per lo zero, con 1 – 3 – 9 per il 2, con 1 – 3 – 7 per il 4, con 3 – 7 – 9 per il 6, per 1 – 7 – 9 per l’8
Prendiamo ad esempio il numero primo 99581. Il numero pari immediatamente successivo è 99600. Se a tale numero pari sottraiamo 99581 otteniamo 19. Se sottraiamo 99577 abbiamo 23. Sottraendo 99571 abbiamo 29. E poi 99563 + 37. 99559 + 41. 99529 +71. 99527 + 73. 99497 + 103.
Aumentando di 2 il numero pari, avremo 99602 – 99559 = 43. 99602 – 99571 = 31. 99602 – 99523 = 79.
Col numero pari 99604 – 99551 =53. 99604 – 99581 = 23 . 99604 -99563 = 41 ed altri ancora.
Col numero pari 99606 – 99527 = 79
Col numero pari 99698 – 99577 = 31
Col numero pari 99610 – 99581 = 29, ma non è il caso di continuare.
Se poi vogliamo ottenere un numero primo dalla somma di tre numeri primi non dobbiamo far altro che aggiungere al numero pari corrispondente alla somma di due numeri primi il primo numero primo che risulta dalla differenza coi numeri primi successivi al numero pari preso in considerazione.
Partendo sempre dal numero 99600, il numero primo successivo è 99607 che risulta dalla somma di una delle coppie di numeri primi che formano 99600 col numero 7, che è primo, come lo sono tutte le differenze a seguire.
Partendo dal numero 99602, le differenze coi numeri primi successivi che siano a loro volta numeri primi, saranno 5 – 41 – 59 – e via di questo passo.
Forse ho solo scoperto l’acqua calda, ma sarei lieto se qualche competente in materia mi potesse fornire qualche chiarimento. Grazie
Solo alcune correzioni:
I numeri primi non possono finire con 0, altrimenti sarebbero pari.
Il numero pari immediatamente successivo a 99581 non è 99600 ma 99582.
Inoltre e vero che sommando due soli primi dispari si possono formare infiniti pari, ma non è detto che siano proprio tutti, potrebbero mancarne alcuni oppure infiniti, qui sta la difficoltà della dimostrazione, provare che non si salta neppure un primo, e non statisticamente. Saluti
Una domanda cos’è che ha portato a scegliere il numero 3 da sottrarre al numero dispari?
Ho dato una scorsa alla “dimostrazione” proposta da Francesco, ma non riesco a capire dove sta la dimostrazione, posto che come detto da Alessandro Zaccagnini, non è sufficiente argomentare statisticamente per dare una dimostrazione assoluta.
peggio: sembra dimostrare solo che – con probabilità vicino ad 1 – la somma di due primi è un numero naturale!
Caro roberto ,sono consapevole dei miei limiti,ma vorrei farti notare che se con 24 primi abbiamo 576 possibili combinazioni;con 167 abbiamo 27.889
possibili combinazioni;con 1.228 abbiamo 1.507.984 possibili combinazioni.
Io credo che abbiamo sufficienti numeri primi per ottenere qualsiasi numero pari.
Con pigreco di N: possiamo ottenere tutti i primi fino ad N
possiamo ottenere molti primi fino a 2pigreco N
non possiamo ottenere i numeri pari oltre questo.
Ti sarei grato se mi potessi indicare quale sia la maggiore difficoltà
di questa congettura
Questa argomentazione mostra che un numero pari “tipico” ha molte rappresentazioni come somma di due numeri primi, perche’ i numeri primi sono sufficientemente numerosi. Versioni quantitative sempre piu’ precise di questo fatto sono state ottenute durante tutto il corso del XX secolo. L’ultima e` stata data da Jànos Pintz nel 2006. Il problema principale e` che questa e` solo un’affermazione di tipo statistico e, molto in generale, non e` possibile dedurre il valore di un attributo di un singolo elemento di una popolazione sapendo solo il valore medio di questo attributo su tutta la popolazione. In altre parole, quello che vale per un elemento “tipico” potrebbe non valere per qualche rarissimo elemento “atipico” o “eccezionale”. Nel caso del problema di Goldbach, per quanto se ne sa oggi potrebbero esistere infiniti numeri pari non rappresentabili come somma di due numeri primi (nessuno ci crede, ma non si puo` escludere): questi numeri “eccezionali”, ammesso che esistano, sono rarissimi e sfuggono alle argomentazioni di tipo statistico.
Con i numeri primi fino a 97 si possono ottenere quasi tutti i numeri pari fino a 194.Tpltp 2 che non serve al caso sono 24 i numeri primi
fino a 100;con questi possiamo ottenere 300 numeri pari alcuni anche più di una volta.
Con i 168-1=167 primi che si trovano fino a 1000 possiamo ottenere:
(167^2+1679)/2=14.028 numeri pari ;sicuramente tutti i numeri pari fino a 1000.
Conoscrndo i numeri primi fino ad un numero di 17 milioni di cifre
possiamo ottenere tutti i numeri pari fini a numeri di questa grandezza.
Il limite è dato dalla conoscenza dei primi,ma poichè i primi sono infiniti con essi possiamo ottenere gli infini numeri pari.
Caro Mario Menin, la frase “Il limite è dato dalla conoscenza dei primi,ma poiché i primi sono infiniti con essi possiamo ottenere gli infini numeri pari”,
non è una dimostrazione. Al massimo è un buon auspicio. A oggi la congettura di Goldbach forte (ogni numero pari maggiore di 2 può essere
scritto come somma di due numeri primi) è un problema aperto e difficile della matematica. Il migliore risultato conosciuto è conseguenza del risultato di Helfgott del 2013 (non ancora pubblicato), che ha risolto la congettura di Goldbach debole, dimostrando così tra l’altro che ogni numero pari è al massimo composto dalla somma di 4 numeri primi. Insomma, ancora tanto lavoro per arrivare alla fine.
Fino a 100 li conosciamo i primi perchè fermarsi a 53!
Che cosa ci impedisce di adoperare un numero primo anche più volte,esso mantiene sempre le sue caratteristiche;purchè si rispetti il dettato della congettura.
La foto da voi pubblicata non mi sembra quella di Goldbach, ma quella di Grossman. Potete controllare? Grazie, Francesco
Vero, già segnalato qui: http://utenti.quipo.it/base5/diarioB5/diario2010.htm. Ci scusiamo dell’errore e provvediamo subito. Grazie!
Questo è il link esatto del nostro crivello di Eratostene bidimensionale per la congettura di Goldbach:
http://www.giovanniarmillotta.it/metodo/grafico02.jpg
estendendo tale crivello a numeri più grandi, tutti i numeri pari risultano , almeno una volta (e soprattutto sempre più volte, specie i numeri par N di forma 6k come fattoriali e soprattutto primoriali) come somma di due numeri primi sempre più grandi, e senza contro esempi, per cui la congettura e vera, e anche quella (cosiddetta debole) per tre numeri primi con somma N dispari), per la quale è valido un crivello di Eratostene tridimensionale, difficile da disegnare, ma funziona allo stesso modo.
Francesco
Penso che le tabelle di cui sopra (tavole di addizione dei numeri primi)e che riguardano la congettura di Goldbach, siano tratte da una nostra proposta di dimostrazione. O forse potrebbe essere una scoperta indipendente di qualcun altro. In ogni caso, l’importante è che si sia finalmente capito bene il meccanismo: un crivello di Eratostene bidimensionale. Ecco il link con la nostra tabella originale, dalla quale, eliminando le righe e le colonne eliminate (perche partono da numeri composti, si ottengono le tabelle da voi pubblicate:
http://www.giovanniarmillotta.it/metodo/grafico01.jpg
A tutti gli interessati, buona lettura! Francesco
Il link esatto della nostra dimostrazione è il seguente :
http://www.giovanniarmillotta.it/metodo/di_noto14.html – 76k
Francesco
Ottimo articolo su Goldbach. Ma attenzione a sottovalutarne l’importanza. Apparentemente non serve a nulla o a ben poco, ma non è affatto così perchè, conoscendola bene (la studio da dieci anni e più) , ho notato un filo rosso matematico che attraversa altre due congetture simili (primi gemelli e Sophie Germain)e potrebbe in futuro arrivare ad una fattorizzazione più veloce,e forse anche all’ipotesi di Riemann RH , tramite l’ipotesi equivalente RH1 (similitudine di grafici come,ecc…Ci lavorerò ancora nei prossimi anni.
Ovviamente, la ritengo vera, come pure la congettura debole (N dispari come somma di tre primi)
Francesco