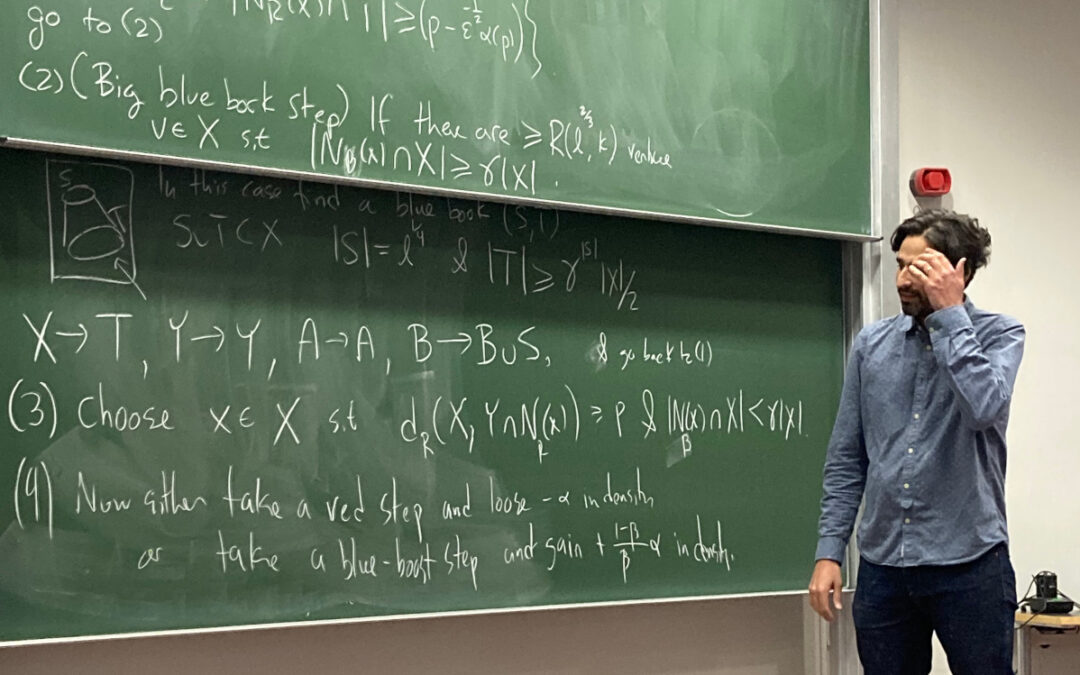È da poco stato annunciato un nuovo risultato sulla teoria di Ramsey. Di che si tratta? E cosa c’entra Erdős? Ce lo racconta Alessandro Zaccagnini.
Su MaddMaths! abbiamo spesso parlato del matematico ungherese Pál Erdős, una delle figure piú interessanti del XX secolo. Erdős ha scritto oltre 1500 articoli con oltre 500 collaboratori e i suoi interessi hanno toccato principalmente la teoria dei numeri, la probabilità e la combinatoria. La sua eredità non comprende solo le migliaia di teoremi che ha dimostrato, ma anche una quantità di problemi aperti la cui soluzione ha stimolato e continua a stimolare generazioni di matematici. Ho parlato della soluzione di due di questi problemi in Teoria dei Numeri proprio qui, in un paio di articoli [1 ]A. Zaccagnini, 2015. “Terence Tao Dimostra Una Congettura Di Erdős (with a Little Help from His Friends).” Sito Web MaddMaths! https://maddmaths.simai.eu/divulgazione/focus/terence-tao-erdos/, [2 ]A. Zaccagnini, 2022. “Un Problema Di Erdős.” Sito Web MaddMaths! https://maddmaths.simai.eu/ricerca/un-problema-di-erdos/.. Una caratteristica peculiare di molti problemi di Erdős è l’apparente semplicità della formulazione, che spesso nasconde una diabolica difficoltà della soluzione.
La notizia del giorno riguarda un problema di combinatoria e precisamente che riguarda la teoria di Ramsey. La formulazione matematica riguarda la colorazione dei grafi, ma possiamo darne una versione piú accessibile pensando ad una cena con tanti invitati. Supponiamo che due invitati siano amici oppure estranei. La domanda è questa: quanto deve essere grande il numero \(R\) degli invitati alla cena, affinché esista sicuramente un insieme di 3 invitati che sono tutti amici oppure tutti estranei uno all’altro?
Se gli invitati sono solo 5 e ciascuno conosce solo i propri vicini di tavolo, non è troppo difficile convincersi con un disegno che non si verifica nessuna delle due alternative della domanda precedente. Dunque \(R > 5\).
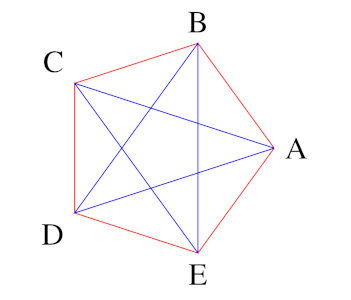
Ciascun commensale conosce i suoi due vicini, e nessun altro: la conoscenza è indicata da un segmento rosso, l’estraneità da un segmento blu. Se gli invitati sono 6, A, B, C, D, E, F, allora ne scegliamo uno, diciamo A. A conosce almeno tre fra gli altri invitati oppure è estraneo ad almeno tre degli altri invitati. I due casi sono simmetrici e consideriamo il primo: diciamo che A conosce B, C e D.
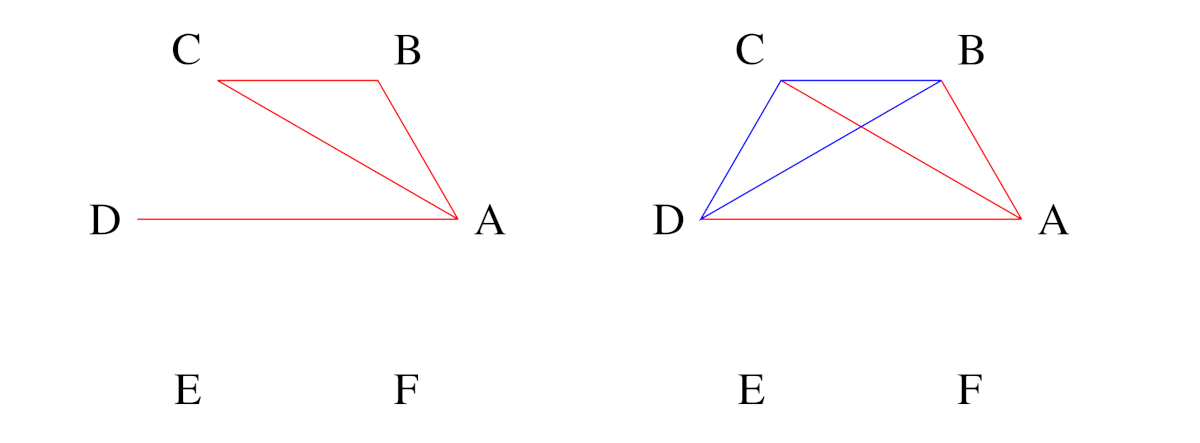
Se almeno due fra B, C e D si conoscono (B e C nella nostra figura a sinistra), abbiamo l’insieme di 3 invitati che si conoscono reciprocamente. Se invece B, C e D sono estranei fra loro, abbiamo lo stesso risolto il problema.
In generale, fissiamo il numero intero positivo \(k\) al posto del numero 3 dell’esempio precedente e ci chiediamo quale sia il minimo intero \(R(k)\) per il quale si possa essere certi che ad una cena con \(R(k)\) invitati nella quale valgono le condizioni già enunciate esistono almeno \(k\) invitati che si conoscano reciprocamente o che siano tutti estranei fra loro. La domanda di Erdős riguarda la velocità di crescita di \(R(k)\) come funzione di \(k\) quando \(k\) cresce senza limite. Siccome è molto difficile determinare il valore esatto di \(R(k)\) quando \(k\) è grande, ci si accontenta di determinare maggiorazioni e minorazioni per il suo valore; in altre parole, vogliamo sapere quanti invitati sono sufficienti (e quindi stimare \(R(k)\) dall’alto) e quanti sono necessari (e quindi stimare \(R(k)\) dal basso). E naturalmente ci piacerebbe che queste due stime fossero piuttosto vicine fra loro, in modo da lasciarci relativamente poca incertezza sul valore esatto di \(R(k)\).
Nell’esempio con \(k = 3\) abbiamo visto che 5 invitati non bastano, perché c’è almeno una configurazione di 5 invitati in cui non succede quello che chiediamo; dunque \(R(3) > 5\). Abbiamo anche visto che qualunque insieme con 6 invitati contiene un sottoinsieme con la caratteristica voluta; dunque \(R(3) \le 6\) e in definitiva \(R(3) = 6\). In generale, per \(k\) grande le due limitazioni inferiore e superiore non permettono di determinare il valore esatto di \(R(k)\); le migliori stime note per \(k = 5\) sono \(43 \le R(5) \le 48\).
Semplificando un po’, la minorazione e la maggiorazione per \(R(k)\) sono entrambe funzioni esponenziali in \(k\), ma con basi molto diverse. Piú precisamente, Erdős ha dimostrato nel 1947 che \(R(k) \ge \frac k{e \sqrt{2}} 2^{k / 2}\) per \(k\) grande. Per questa dimostrazione, fra i primi nella storia, ha usato dei metodi di natura probabilistica. I grandi matematici spesso gettano ponti fra aree apparentemente sconnesse della matematica, mostrandone la fondamentale unità.
Per dimostrare la maggiorazione \(R(k) \le \frac{4^{k – 1}}{\sqrt{\pi k}}\), Erdős e il suo collaboratore Szekeres hanno invece utilizzato alcune proprietà dei coefficienti binomiali!
Riassumendo e semplificando, questo significa che \(\bigl(\sqrt{2}\bigr)^k < R(k) < 4^k\) per \(k\) grande, come dicevamo. Abbiamo dunque costretto \(R(k)\) fra due funzioni esponenziali, ma le basi di queste funzioni sono molto diverse fra loro e per \(k\) grande l’incertezza sul valore reale di \(R(k)\) aumenta velocemente.
Ci sono stati alcuni miglioramenti di queste stime, negli ultimi decenni, tutti relativamente piccoli. Ha dunque suscitato l’entusiasmo di Timothy Gowers, che ha ricevuto la Medaglia Fields nel 1998 proprio per i suoi studi in combinatoria, l’annuncio fatto la settimana scorsa da Marcelo Campos, Simon Griffiths, Robert Morris e Julian Sahasrabudhe di essere riusciti ad abbassare la stima dall’alto sostituendo il valore \(4\) con \(3.9995\) in un nuovo preprint appena sottomesso [3 ]M. Campos, S. Griffiths, R. Morris, & J. Sahasrabudhe. 2023. “An Exponential Improvement for Diagonal Ramsey.” https://arxiv.org/abs/2303.09521.. Apparentemente si tratta di un piccolo miglioramento, ma è il primo del suo genere dal 1935 e inoltre gli autori stessi si dichiarano certi che sia possibile ridurre ulteriormente la costante \(3.9995\) ad un valore piú piccolo.
Nel suo lungo post su Twitter, Gowers rivela di essere stato presente al seminario tenuto da Julian Sahasrabudhe nel quale questo risultato è stato annunciato; il titolo non ha destato sospetti, essendo “On an old problem of Erdős”!
I was at a sensational combinatorics seminar in Cambridge yesterday, reminiscent of the time I had been tipped off that Andrew Wiles’s seminar at the Newton Institute on Wednesday 23rd June 1993 might be worth going to. 🧵https://t.co/rDj3KA4MPO
— Timothy Gowers @wtgowers@mathstodon.xyz (@wtgowers) March 17, 2023
Un commento interessante di Gowers è questo: ” Durante il seminario ero preoccupato di poter avere la sensazione che se solo avessi pensato un po’ più intensamente a un certo punto della mia vita avrei potuto risolvere il problema da solo. Ma non ho avuto affatto quella sensazione: la dimostrazione era molto diversa dal tipo di argomentazione che avevo cercato di trovare, e non credo che l’avrei mai trovata. Quindi, anche se un piccolo sogno muore, sono molto felice di vedere questa svolta.”
Alessandro Zaccagnini
Per chi vuole approfondire.
Si può consultare la pagina di wikipedia https://it.wikipedia.org/wiki/Teorema_di_Ramsey; la versione inglese è piú dettagliata, ma anche quella italiana è molto ricca di informazioni. Una vivace esposizione dei problemi trattati qui si trova nei due articoli di Roberto Zanasi apparsi su Archimede e ora accessibili sul suo blog [4 ]R. Zanasi, 2018. “Minacce aliene, prima parte.” http://proooof.blogspot.com/2018/09/minacce-aliene-parte-1.html., [5 ]R. Zanasi, 2018. “Minacce aliene, seconda parte.” http://proooof.blogspot.com/2018/10/minacce-aliene-2.html..
Immagine di copertina: uno degli autori, Julian Sahasrabudhe, durante il seminario a Cambridge il 17 marzo. Foto ripresa dal tweet di T. Gowers citato nel testo.
Note e riferimenti
| ⇧1 | A. Zaccagnini, 2015. “Terence Tao Dimostra Una Congettura Di Erdős (with a Little Help from His Friends).” Sito Web MaddMaths! https://maddmaths.simai.eu/divulgazione/focus/terence-tao-erdos/ |
|---|---|
| ⇧2 | A. Zaccagnini, 2022. “Un Problema Di Erdős.” Sito Web MaddMaths! https://maddmaths.simai.eu/ricerca/un-problema-di-erdos/. |
| ⇧3 | M. Campos, S. Griffiths, R. Morris, & J. Sahasrabudhe. 2023. “An Exponential Improvement for Diagonal Ramsey.” https://arxiv.org/abs/2303.09521. |
| ⇧4 | R. Zanasi, 2018. “Minacce aliene, prima parte.” http://proooof.blogspot.com/2018/09/minacce-aliene-parte-1.html. |
| ⇧5 | R. Zanasi, 2018. “Minacce aliene, seconda parte.” http://proooof.blogspot.com/2018/10/minacce-aliene-2.html. |