Generalmente l’esponenziale (e la sua controparte: il logaritmo) è considerato un oggetto ”difficile”, da rifuggire, se possibile. Tranne nel diffuso modo di dire ”crescita esponenziale”.
Proviamo a partire proprio da qui. Supponiamo di voler controllare la crescita di una popolazione come, ad esempio, quella dei conigli, forse perché ci interessa investire in questo settore o forse per pura curiosità scientifica. Non e’ rilevante. Quello che ci interessa, evidentemente, è sapere anno per anno (o mese per mese) quanti conigli abbiamo, ma  l’oggetto più importante che vogliamo conoscere è quale sia la variazione di conigli da un anno al successivo (quindi la differenza tra i conigli del 2009 e quelli del 2010, per esempio).
Un modello predittivo che ci dica quanti conigli abbiamo deve indicarci quanto vale questo incremento. Un primo modello semplicissimo potrebbe per esempio asserire che la variazione è costante: ogni anno produciamo 10 conigli in più. La crescita finale, allora, sarà facilmente calcolabile: 10 conigli all’anno, quindi al secondo anno avremo 10 conigli più quelli iniziali, al terzo 20 e così via. Ci sarà cioè una crescita lineare (in un grafico anni/numero di conigli) e il grafico che rappresentasse questa situazione sarà una retta.
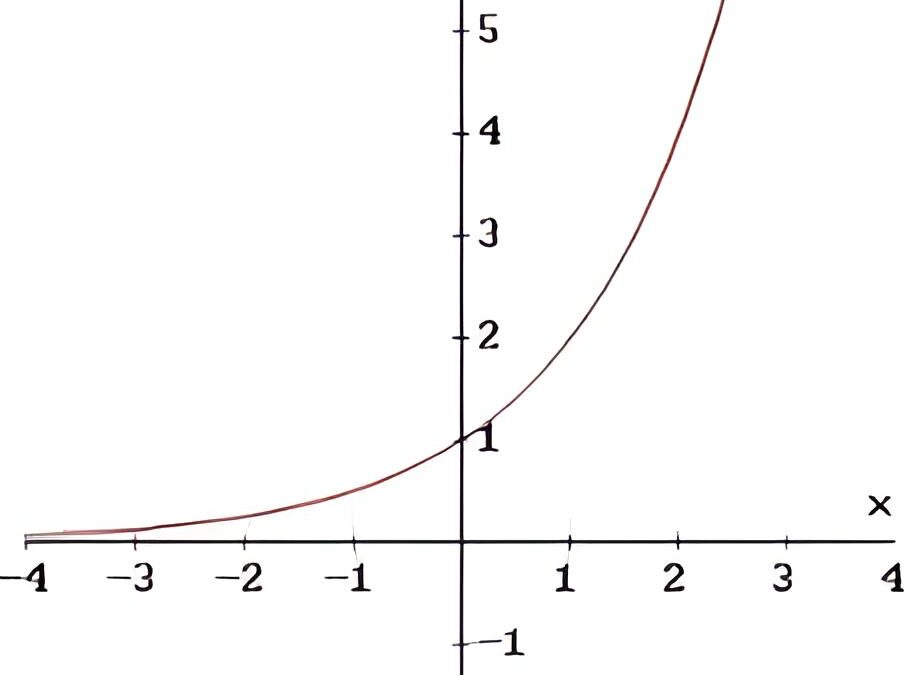
Ma questo modello non è poi così convincente, dato che più conigli abbiamo e più ne nascono! Quindi se 10 è il numero di conigli prodotti da una coppia di conigli, per ogni anno avremo un incremento pari a 10 moltiplicato il numero di coppie. Ovvero, più coppie abbiamo e più la nostra produzione annuale aumenterà! Il quadro finale fornito da questo nuovo modello è proprio quello di una crescita esponenziale, cioè qualcosa del tipo 10 elevato alla n: 10 per 10 per 10 per 10… per il numero di anni trascorsi. Lo stesso tipo di meccanismo si ritrova anche nei conti bancari. Ogni anno la banca dà un ”bonus”, che è legato al fatto che abbiamo depositato i nostri soldi. Il ”bonus” non è indipendente da quanti
soldi abbiamo, ma è proporzionale al deposito stesso. Quello che viene indicato, infatti, non è la variazione assoluta del conto di anno in anno, ma il cosiddetto “tasso di interesse”, ossia il rapporto tra la variazione assoluta e il valore del deposito. Questo sistema corrisponde esattamente al modello di crescita esponenziale dei conigli. Se quindi ci chiediamo come mai non notiamo una crescita abissale del nostro conto in banca… la risposta è ricavabile ragionando come nel problema dei conigli: 1 per 1 per 1 per 1 per 1 per il numero di anni trascorsi, fa sempre 1. Cioè alla fine si ritrova il deposito iniziale. In concreto, nel calcolo bisogna sostituire ad 1 un numero leggermente più grande, ma la sostanza non cambia di molto… (la crescita non è così rapida come ci piacerebbe!).In matematica, per motivi che non si possono spiegare in due parole, è particolarmente interessante l’esponenziale che ha per base il cosiddetto numero di Nepero, che si indica con e. Quindi, per esempio, interessa sapere quanto fa e per e per e per e…
Si tratta di un numero magico tanto quanto pi greco, che ricorre in diverse situazioni e che per questo riscuote particolare popolarità nell’ambiente. Anche e, come pi greco è un numero irrazionale, cioè i suoi decimali non hanno nessuna forma di periodicità.

Accenniamo, infine, a un altro tasto dolente: il logaritmo. Da dove viene fuori? Dallo stesso meccanismo per cui se sappiamo sommare, rapidamente ci viene voglia e necessità di sottrarre. E se sappiamo moltiplicare, di dividere. Sottrarre e dividere sono le operazioni inverse di sommare e moltiplicare, rispettivamente. Sostanzialmente, se sommare e moltiplicare corrispondono a mettere disordine in camera, sottrarre e moltiplicare corrispondono a mettere in ordine, cioè riconducono al punto di partenza. Allo stesso modo, il logaritmo è l’operazione inversa dell’esponenziale, e quindi per risolvere problemi in cui compaiano esponenziali è indispensabile il loro uso. Quello che l’esponenziale sposta di posto, il logaritmo rimette in ordine. Comodo, no?