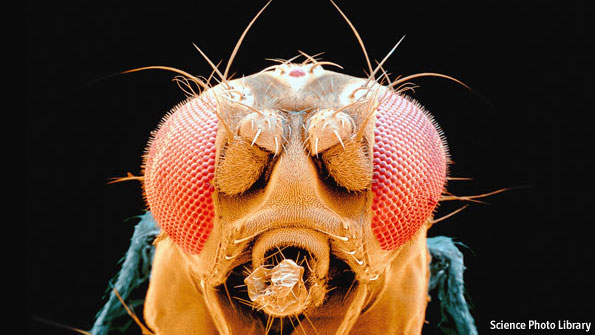
Neppure dopo il morso di una velenosa mela al cianuro, Alan Turing riesce a riposare tranquillo. Questa volta è il ronzio di una specie di mosca a disturbare il suo riposo. Colpa (o merito) di un gruppo di ricerca russo che sostiene, in questo articolo, di aver visto strutture di Turing nella cornea di una Drosophila, insetto noto anche come moscerino della frutta. Guardare negli occhi un animale di dimensioni così piccole, pur se non richiede grande coraggio (una forma di confronto tra Davide e Golia, visto dalla parte di Golia), non è cosa da poco perché le misure sono nanometriche. Pertanto, quel che si vede sono nanostrutture. Nanostrutture di Turing, dichiarano Blagodatski e colleghi. La coincidenza con i nani di Biancaneve è puramente accidentale.

di Corrado Mascia e Davide Palmigiani

Lasciamo in stand-by gli scienziati russi e facciamo un salto indietro nel tempo. Quasi cento anni fa, sir D’Arcy Wentworth Thompson dichiara nella prefazione del suo “On growth and form”, che “non è il biologo con l’inclinazione alla matematica, ma il matematico esperto e colto che deve fare i conti con problemi come sono abbozzati ed adombrati qui”. D’Arcy si riferisce al problema della morfogenesi, cioè dell’origine delle forme biologiche. A sentir lui, spiegare l’emergere di strutture complesse a partire da un conglomerato di cellule inizialmente indifferenziate è questione di matematica.

Superate un paio di guerre mondiali, nel 1952, Alan Turing pubblica “The chemical basis of morphogenesis”, una vera e propria pietra miliare della bio-matematica. Ne abbiamo già parlato qualche mese fa su MaddMaths!, qui, e vi invitiamo a leggere l’articolo prima di proseguire. Comunque ecco i punti salienti:

“Si suggerisce che un sistema di sostanze chimiche, chiamate morfogeni, possa essere adeguato a descrivere il fenomeno della morfogenesi…”
Meditando attorno all’idea di trovare meccanismi semplici che producano risposte complesse, Turing propone un modello in grado di spiegare la morfogenesi. Come è possibile che la Vita si auto-organizzi? Come si arriva dalla semplice struttura simmetrica di uno zigote alla complessità di un individuo maturo?

“Equazioni di reazione-diffusione”
Turing assume che esistano due classi di agenti chimici, detti morfogeni, che abbiano due comportamenti fondamentali: entrambe possono spostarsi all’interno dell’organismo (diffusione), tendendo a “spalmarsi” in maniera omogenea. Una delle due sostanze, detta attivatore, accende un meccanismo di formazione (ad esempio, la pigmentazione della pelle), l’altra, detta inibitore, lo spegne. In aggiunta, attivatore ed inibitore interagiscono tra loro (reazione) secondo un meccanismo di tipo chimico descritto da una funzione matematica opportuna (razionale, di frequente, e polinomiale, nei casi più semplici).

“Instabilità di Turing”
Quando diffusione e reazione vengono considerate singolarmente, la differenziazione non si manifesta. Tutto tende verso una distribuzione uniforme degna del più noioso dei mondi. Lo straordinario sta nel fatto che la compresenza di reattività e diffusività dà luogo a risultati inaspettati. Il modello, per sua natura, genera un insieme di onde di concentrazione (di attivatore e di inibitore) che si amplificano nel tempo generando differenze a partire da un tutt’uno originariamente indistinto. Tale fenomeno, che è il fulcro dell’articolo del 1952, prende il nome di “Instabilità di Turing”.

“I serpenti sono generalmente a strisce e non a pallini”
Come mostrato poi da J. D. Murray in un articolo divulgativo del 1988, questo tipo di schema è in grado di mostrare, in linea teorica, come si determinino le colorazioni delle livree degli animali, come le macchie dei leopardi, le strisce delle zebre, così via dicendo.

Resta però una domanda di base: il meccanismo di Turing, che è in grado di esibire strutture complesse da regole semplice, è davvero alla base della formazione di strutture reali? L’analogia della forma generata dal modello matematico e dall’esperimento fisico non garantisce nulla riguardo al meccanismo di generazione che, alle volte, potrebbe essere puramente accidentale. Ad esempio, con l’iterazione di una trasformazione opportuna, è possibile generare un disegno, una  montagna frattale, simile (davvero di molto) ad una vera montagna. Ma la maniera con cui le montagne reali si formano e quella con cui le montagne frattali si generano sono ben distinte. Se ne deduce che si tratta di una coincidenza di eventi, piuttosto che di una connessione nascosta (vedi qui altre informazioni su questo argomento).

Dunque, tornando all’instabilità di Turing, se è vero da un lato che le forme generate (al variare dei parametri in gioco) sono variegate e analoghe ad alcune forme della natura, resta la questione dello stabilire se la relazione attivatore-inibitore sia un fatto reale o un’allegra fantasia matematica. Ne nasce una caccia al morfogene, analoga alla più famosa caccia al Bosone di Higgs. Va sottolineato, però, che se si usasse lo stesso standard di certezza richiesto dai fisici delle alte energie per attestare la tangibilità della teoria (con una probabilità di errore non superiore a una parte su centomila) non ci sarebbe speranza per nessuno di validare il meccanismo di Turing. Il mondo del vivente è ben più difficile della materia nuda e cruda. Per certi versi, individuare casi reali in cui una struttura eterogenea sia determinata dalla presenza di un sottostante meccanismo di reazione-diffusione è una caccia al Sacro Graal. Diversi gruppi di ricercatori hanno contribuito con le loro scoperte, interpretandole come manifestazione reale del meccanismo teorico di Turing. Nel 1990, V.Castets e collaboratori, nello studio di una reazione chimica di tipo CIMA riportano la prima “comprovata” evidenza sperimentale della presenza di strutture alla Turing. Nel 1995, Kondo e Asai sostengono di rilevare onde di reazione-diffusione sulla pelle del pesce angelo Pomacanthus. E così via dicendo.

Si inserisce nel filone il gruppo di ricerca russo di cui si diceva all’inizio. Il punto di partenza è piuttosto quello di un’analogia di immagini. L’esplorazione delle strutture corneali nano-metriche di un certo numero di insetti porta alla luce strutture di vario genere: pois, strisce, forme labirintiche. La corrispondenza con forme analoghe generate da modelli di reazione-diffusione è notevole. Suggerisce, come per la serie di studi sul pesce angelo, che una connessione ci possa essere e che valga la pena continuare l’esplorazione, cercando di capire meglio quali siano gli agenti ed i meccanismi che determinano la formazione di queste strutture e se e come siano traducibili nel formalismo matematico delle equazioni differenziali. Per ora, a leggere il lavoro, il dettaglio matematico resta generico. Non viene precisata quale espressione funzionale sia quella che determina le simulazioni utilizzate per paragonare la misurazione sperimentale con il modello teorico, né se tale espressione sia scelta ad hoc (cioè per formare la struttura che si vuole vedere) o se sia il risultato di una ipotesi di meccanismo di formazione corneale. Insomma, la storia sembra essere solo all’inizio. E, con buona probabilità, Turing sarà costretto, ancora per un po’, a tenere d’occhio il volo esasperante di un minuto moscerino della frutta.

Riferimenti bibliografici

A.Blagodatski, A.Sergeev, M.Kryuchkov, Y.Lopatina, V.L.Katanev. Diverse set of Turing nanopatterns coat corneae across insect lineages. Proceedings of the National Academy of Sciences 112, no. 34 (2015), 10750-10755.

V.Castets, E.Dulos, J.Boissonade, P.De Kepper. Experimental evidence of a sustained standing Turing-type nonequilibrium chemical pattern. Physical Review Letters 64, no.24 (1990) 2953-2955.

S.Kondo, R.Asal. A reaction-diffusion wave on the skin of the marine angelfish Pomacanthus. Nature 376 (1995) 765-768.

S.Kondo, T.Miura. Reaction-diffusion model as a framework for understanding biological pattern formation. Science 329 (2010) 1616-1620.

J.D.Murray. How the leopard gets its spots. Scientific American 258, no. 3 (1988), 80-87.

J.D.Murray, Why are there no 3-headed monsters? Mathematical modeling in Biology. Notices of the American Mathematcal Society 59, no.6 (2012), 785-795.

A. Turing, The chemical basis of morphogenesis, Philosphical Transactions of the Royal Society of London, Series B, Biological Sciences, vol. 237, issue 641 (1952), 37-72.