In questo articolo realizzato da Francesco Ferrari, Giulia Franchi, Stefano Gasparotto, Beatrice Minorini, Rebecca Rossi della Classe IV AS del Liceo Scientifico Statale, “Marie Curie” di Tradate (VA), sotto la supervisione dalla Prof.ssa Francesca E. Magni, i ragazzi si sono interrogati su quanta matematica contenga un semplice orologio.

---

In questo articolo abbiamo voluto analizzare il comportamento dell’orologio analogico, un oggetto comune che presenta intrinseche proprietà matematiche nel suo funzionamento. Abbiamo trovato, in particolare, collegamenti con l’aritmetica modulare, con i numeri complessi, le funzioni goniometriche, quelle composte e quelle a valori in N.

Sono le 9:00 del mattino. Marco telefona a Laura: “Ti aspetto al supermercato tra 8 ore per comprare l’occorrente per il party: bibite, salatini, stelle filanti e un prosciutto di Parma D.O.P”. Laura vuole essere sicura che al banco dei salumi ci sia l’amica Ezzelina, l’unica salumiera in grado di tagliare fette dello spessore di $${\pi}\over{6}$$ millimetri. Il turno di Ezzelina è dalle 4 alle 8 di pomeriggio. Laura ora farà dei calcoli per scoprire l’ora esatta dell’appuntamento. Se non ci sarà Ezzelina al banco salumi sarà costretta a cambiare l’orario datole da Marco. E in men che non si dica, risponde che le 5 di pomeriggio è un orario perfetto. Come fa 8+9 a fare 5? Laura fortunatamente conosce la matematica modulare! Scopriamola insieme.

Laura aggiunge 8 ore alle 9 attuali, ottenendo così 17. Sul quadrante di un orologio ci sono 12 ore. Eseguendo $${17}\over{12}$$si ottiene come resto 5. Quando la lancetta delle ore supera il 12, il conteggio riparte da capo. Il numero su cui la lancetta delle ore si ferma, è il resto di tale divisione. Per scoprire il perché di questo fenomeno dobbiamo studiare l’aritmetica modulare.

Ma prima un po’ di storia… Gauss all’età di diciannove anni, dopo aver scoperto una magnifica costruzione geometrica di una figura con diciassette lati, decise di iniziare un diario matematico che avrebbe poi tenuto per i successivi diciassette anni. In questo diario compare la sua invenzione del “calcolatore a orologio”, un’idea che permetteva di semplificare i calcoli con numeri molto grandi grazie allo stesso principio di un normale orologio.

Nel 1801 introdusse il calcolo modulare nel suo libro “Disquisitiones Arithmeticae”. Egli raccolse qui i risultati della teoria dei numeri ottenuti da matematici del calibro di Eulero, Lagrange e Legendre, aggiungendovi importanti nuovi contributi. Tra le novità di questo testo si trovano il concetto di modulo e la notazione $$a\equiv b (mod\text{ } n)$$ .

L’aritmetica di Gauss rivoluzionò la matematica del XIX secolo e ancora oggi è fondamentale per la sicurezza in Internet, dove si utilizzano orologi con un numero di ore che supera quello degli atomi esistenti nell’universo osservabile. Oggi infatti in informatica viene comunemente utilizzata la chiave di decrittazione AES a 256bit, che è basata sullo stesso funzionamento dell’aritmetica dell’orologio: vengono generate delle chiavi univoche a partire dalla password inserita che il computer è impostato per decrittare.

Una delle prime e più importanti applicazioni di questa branca della matematica fu ideata da Pierre de Fermat già a metà del 1600, con il “piccolo teorema di Fermat”, che afferma: se p è un numero primo, allora per ogni intero a abbiamo: 

$$ a^p\equiv a (mod\text{ } p)$$

che, dividendo per a≠0 , può essere espresso nella forma

$$ a^{p-1}\equiv 1 (mod\text{ } p)$$.

Ad esempio, $$ 8^5\equiv 8 (mod\text{ }5)$$, e quindi $$ 8^4\equiv 1 (mod\text{ }5)$$.

L’aritmetica modulare è un sistema di aritmetica degli interi nel quale i numeri “si avvolgono su stessi” ogni volta che raggiungono i multipli di un determinato numero n detto modulo.

Fissato un modulo n e un numero intero k possiamo calcolare il valore di $$ k (mod\text{ } n) $$ come il resto r della divisione $$\frac{k}{n}$$, ossia il numero tale che $$r+nq=k$$, dove q è il quoziente intero della divisione, di cui però non ci occuperemo ai fini della matematica modulare. Ad esempio, dato un modulo n, esistono infiniti valori k che danno tutti uno stesso resto r, quindi il valore di q non ci interessa, essendo r l’unico elemento significativo. Infatti, nel caso dell’orologio, in genere a noi interessa soltanto sapere qual è il numero risultante dall’operazione di modulo, non il numero di giri che compie la lancetta prima di arrivarci.

Orologi e funzioni

La matematica modulare trova applicazione negli orologi analogici.

Ci siamo chiesti: “esiste una funzione che descriva analiticamente l’andamento delle lancette?’ Ovviamente sì! Non si tratta però di una funzione “classica” (di quelle cioè che studiamo a scuola, che di solito sono funzioni reali a variabile reale e quasi sempre continue) perché, per esempio, il suo grafico non è descrivibile con una linea continua, ma solo tramite dei punti isolati.

Per quanto riguarda la lancetta delle ore, si ottiene il seguente grafico:

Il grafico è costituito dai punti P (con ascissa unicamente naturale), appartenenti al fascio di semirette parallele alla bisettrice del I e del III quadrante (ossia con coefficiente angolare uguale a 1), originate nei punti dell’asse x rispettivamente (0;0), (12;0), (24;0), …

Il dominio D di questa funzione è l’insieme dei numeri naturali (corrispondente ai valori delle ore) e il codominio è $$C=\{y \in N | 0\leq y\leq 11 \}$$, ossia l’insieme dei numeri corrispondenti alle posizioni y della lancetta sul quadrante dell’orologio. 

Se il modulo è 12, perché non consideriamo il numero 12 nel codominio? Semplice: dà resto 0. Se il modulo è n il resto massimo è n-1.

Studiamo ora la posizione delle lancette $$P(x,y)$$ in funzione del tempo $$t$$, con lo scopo di realizzare un modello matematico che permetta di simulare il loro comportamento. Esiste una relazione tra l’ora segnata dalla lancetta e l’angolo $$\alpha$$ che essa forma al centro dell’orologio in riferimento alle ore 12.

Grazie alle leggi orarie del moto circolare uniforme (la velocita delle lancette è costante) $$\alpha=\omega t$$ e la velocità angolare della lancetta è 

$$\omega={{360^{o}}\over {T}}={{2 \pi}\over {T}}$$

Qui T=12 h perché l’orologio è formato da 12 ore (h), quindi $$\omega={{\pi}\over {6}}{{rad}\over {h}}$$. Allora possiamo ricavare l’angolo $$\alpha$$ spazzato da una lancetta in un $$\Delta t$$ di un’ora:

$$\alpha=\frac{\Delta t\pi} {6}(=\Delta t * 30^{o}).$$

Per disegnare una funzione di questo tipo bisogna scomporre il moto lungo i due assi cartesiani, tramite le equazioni di un moto armonico:

$$x=sen(\frac{\pi}{6}t), \text{ } y=cos(\frac{\pi}{6}t).$$

Secondo la definizione di funzioni goniometriche, il seno dovrebbe riferirsi all’ordinata del punto sulla circonferenza goniometrica, il coseno alla sua ascissa, però, poiché il nostro sistema di riferimento non parte dall’asse x, ma dall’asse y (si pensi all’orologio), per gli archi associati il sistema risulta ruotato di un angolo di $$\frac{\pi}{2}$$ (e tramite le formule degli archi associati si ritrova la definizione “standard”).

La variabile indipendente è il tempo, perché la posizione delle lancette $$P(x,y)$$ dipende unicamente da quello. Si ottiene la rappresentazione/animazione grafica di questo tipo (realizzata con il programma Geogebra) è visualizzabile qui sotto

Possiamo svolgere un ragionamento analogo per la posizione delle lancette dei minuti e dei secondi. Partendo dalla funzione che lega tempo e posizione delle lancette dei secondi possiamo ricavare funzioni che legano i secondi ai minuti, i minuti alle ore, le ore ai giorni eccetera…

È possibile creare funzioni composte che passino direttamente dai secondi alle settimane o dalle ore agli anni, tramite le consuete equivalenze (per esempio: minuti= ore/60 ecc.)

Orologio e numeri complessi

L’aritmetica modulare è connessa anche alle radici dei numeri complessi perché esse si ripetono, data una radice ennesima di z appartenente a $$\mathbb C$$, di un modulo n, dando sempre n risultati. Rappresentando graficamente sul piano di Argand Gauss le soluzioni della radice di indice n di 1, si ottengono dei vettori le cui punte rappresentano i vertici di un poligono regolare di n lati. Nel nostro caso, essendo modulo 12 (12 ore), n=12 e quindi la radice dodicesima di 1 si rappresenta così:

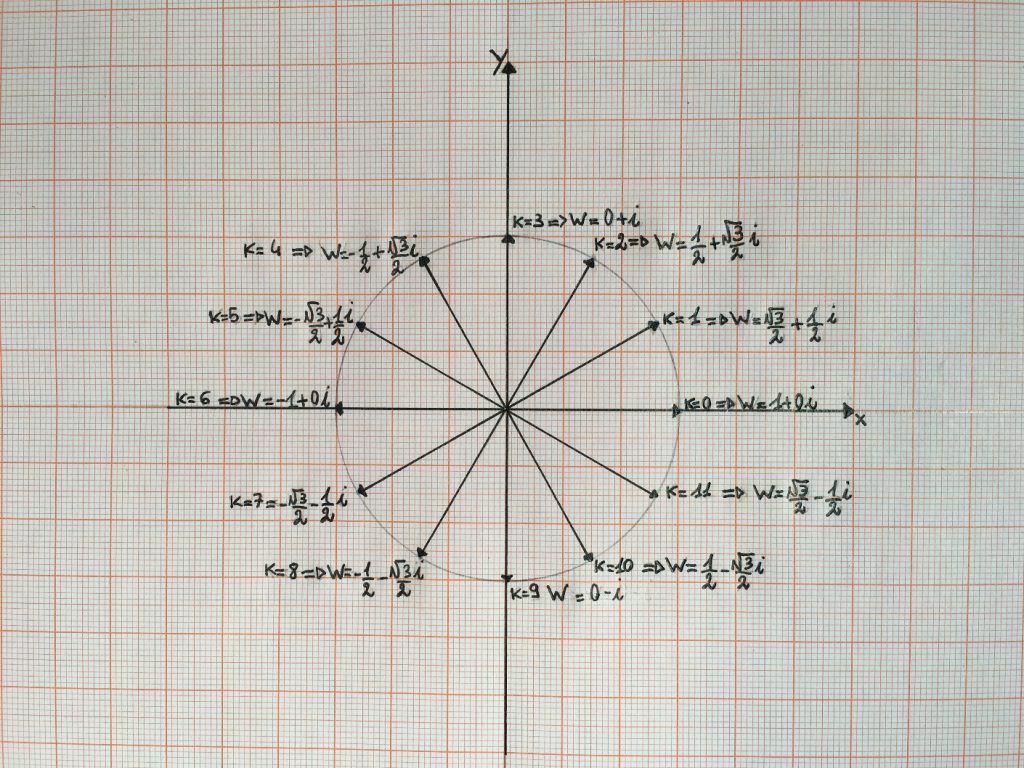
Si può rappresentare la posizione della lancetta delle ore utilizzando il calcolo con i numeri complessi in forma trigonometrica costruendo un vettore, ad esempio:

ore 3 n=12   $$k\equiv(15-3) (mod\text{ } 12)\equiv 0 $$ → $$\sqrt[12]{1}$$ con k=0 sarà il vettore w=1+0i

ore 5 n=12  $$k\equiv(15-5) (mod\text{ } 12)\equiv10 $$ → $$\sqrt[12]{1}$$ con k=10 sarà il vettore w=$$\frac{1}{2}-\frac{\sqrt{3}}{2}i$$

In generale, se vogliamo la posizione della lancetta a un’ora t, possiamo operare trovando k come

$$k \equiv [(3+12h)-t](mod\text{ } 12)$$

con n=12 e h naturale e applicando la formula goniometrica per l’estrazione delle radici n-esime di 1.

La giustificazione di questa formula, che collega le ore alla posizione della lancetta tramite le radici complesse di indice 12 di 1 è la seguente:

• poiché l’orologio convenzionale è ruotato di 90° rispetto al semiasse positivo dell’asse x sul piano cartesiano da cui parte il conteggio degli angoli, bisogna partire da 3 (corrispondente a 3*30°=90°).

• 12h è un fattore irrilevante ai fini del calcolo modulo 12 ma risulta utile per semplificare i calcoli facendo in modo di non usare numeri negativi.

• le ore t vanno sottratte da questo numero perché l’orologio convenzionale procede in senso orario, mentre in matematica si procede in senso antiorario.

Finora si è trattato solo di orologi “classici”, ma lo stesso discorso può essere applicato a un qualsiasi orologio di n ore, in particolare con n=24 si può eliminare il problema dell’incertezza delle ore tra dì e notte, che nel nostro precedente caso si poteva risolvere soltanto con il buon senso o affiancando a.m. e p.m., come da tradizione inglese.

Inoltre, riguardo alle funzioni composte, si possono costruire orologi che tengano conto ad esempio delle settimane in un anno oppure orologi con più lancette che indichino secondi, minuti, ore, giorni, settimane…

Conclusioni: ulteriori applicazioni

L’aritmetica modulare non limita le sue applicazioni agli orologi, ma si può utilizzare per risolvere problemi di vita quotidiana, dove possono essere evitati macchinosi calcoli, applicando la semplice operazione di modulo.

Vediamone un esempio:

il professore di Gauss chiede ai suoi alunni, per tenerli impegnati, di riporre ordinatamente, distribuendo una pallina a cesta per volta, 89 palline in 7 ceste, indicandogli alla fine dove viene posizionata l’ultima pallina. Il piccolo Johann Carl Friedrich si presenta un momento dopo con il risultato, non avendo posizionato alcuna pallina.

Il professore, sbalordito, gli chiede come abbia fatto e il piccolo, gesso in pugno, descrisse l’operazione di divisione $$\frac{89}{7}$$ , indicando come resto 5. Perciò l’ultima pallina sarebbe stata posizionata nella quinta scatola.

Ringraziamo la professoressa Francesca E. Magni che ha sollecitato la nostra curiosità in merito all’argomento e che ci ha consigliato la lettura de “L’enigma dei numeri primi” di Marcus Du Sautoy.