Orgoglio matematico. Guardo la mia scrivania e mi chiedo se ci sia qualcosa di cui dovrei veramente essere orgoglioso. Fogli e libri accatastati gli uni sopra gli altri. In vari strati geologici si trovano progetti di ricerca interessanti ma mai portati a termine, appunti di corsi da completare e ripulire, tesi da rileggere, cose che vorrei studiare senza che trovi il tempo per farlo, una decina di copie del mio curriculum tutte diverse tra loro e servite a soddisfare richieste burocratiche tutte tra loro incoerenti. Ho speso molte ore su questa scrivania e se veramente debba andarne orgoglioso, in qualche misura, ancora non lo so con chiarezza.
In giornate come questa, un po’ di mal di testa da cervicale, una lista infinita di cose da fare e, fuori, un bel sole primaverile, son portato a pensare di no. Non posso farci nulla se il post su Madd:Maths! mi ha sollevato più malesseri esistenziali che entusiasmi giovanili. Deve entrarci qualcosa le età, le fasi della vita, Giove in opposizione, quelle cose così. E poi son pure in ritardo rispetto alla scadenza del Carnevale della Matematica.
Vago un po’ su Internet alla ricerca di materiale didattico per un corso che ancora non sono sicuro di fare – l’ultima delle urgenze a dire il vero – con mille pensieri per la testa quando, casualmente, ritrovo un articolo su cui un mio studente si è spremuto le meningi, come direbbe Paperino, ricavandone per altro un’ottima tesi.
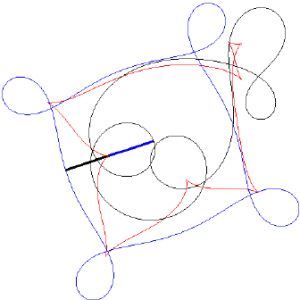
I tracciati blu e nero sono i due possibili tracciati delle ruote anteriori a cui corrisponde lo stesso tracciato posteriore in rosso. Le curve nera e blu sono curve in bicycle correspondence.
Il problema è facile a dirsi, in prima battuta: immaginate di fare una passeggiata e vedere, a un tratto, fuori da una pozzanghera uscire le linee nette tracciate dalle ruote di una bicicletta. Due traiettorie diverse e distinte. Sareste in grado di capire quale delle due traiettorie è disegnata dalla ruota davanti e quale dalla ruota posteriore? E se il tracciato curva e ritorna nella pozzanghera, così da disegnare due curve chiuse sareste in grado di dire in che direzione andava la bicicletta?
Vedi, caro Holmes, direbbe Sherlock – ah, ecco, la citazione non è casuale visto che proprio rispondendo a una domanda di questo tipo si risolve il mistero dell’avventura della scuola del priorato. In effetti il problema non è terribilmente difficile da modellizzare. Essendo la ruota posteriore fissata al telaio, la retta tangente in un punto P al tracciato della ruota posteriore interseca sempre il tracciato della ruota anteriore in un punto f(P) la cui distanza è indipendente da P (è la lunghezza della bicicletta). Si tratta di un vincolo non olonomo in uno spazio di configurazioni tridimensionale, per chi non si fa spaventare da questi termini. Questo permette di scrivere una equazione differenziale abbastanza semplice che lega i due tracciati.
Se pensiamo, dunque, a una bicicletta che viaggi nelle due direzioni opposte percorrendo esattamente lo stesso tracciato con la curva posteriore otteniamo, in generale, due diversi tracciati per la ruota anteriore. Questa si dice essere una coppia di curve in “bicycle correspondence” e la domanda se in qualche caso sia impossibile distinguere la direzione della bicicletta è la domanda se esistano curve in corrispondenza ciclistica con se stesse. E’ il caso della circonferenza. Se la curva anteriore percorre una circonferenza perfetta la curva posteriore percorre anche essa una circonferenza più piccola, non importa se la percorrenza sia in senso orario o antiorario. La circonferenza è l’unica possibilità?

Un esempio di curva di Zindler
La risposta a questa domanda era stata data 80 anni prima che a qualcuno venisse in mente di scrivere le equazioni della bycicle correspondence. Nel famoso “libro scozzese” di Leopoli (l’uso del nome italiano serve a evitare dissidi tra sostenitori della grafia ucraina e di quella polacca), infatti, Ulam si era chiesto se una sfera fosse l’unica forma geometrica in grado di galleggiare nell’acqua stabilmente in qualunque posizione. E la risposta, dimostrò dopo poco tempo, nel ’38, il suo collega Auerbach, è negativa. Esistono delle curve, dette di Zindler, che formano il profilo di corpi con lo stesso tipo di galleggiabilità della sfera. Si tratta di curve con la proprietà che ogni corda che divide l’area della parte interna in due parti uguali è della stessa lunghezza. Della scoperta Auerbach potè gloriarsi poco: fu uno dei matematici polacchi ucciso in un campo di concentramento dalle truppe di occupazione naziste.
Ma l’importanza della equazione non finisce qui. Si tratta di una equazione, quella della corrispondenza ciclistica, che modellizza anche perfettamente il moto degli elettroni in un campo magnetico parabolico e finisce dunque per essere, sotto opportune ipotesi, equivalente a una versione della equazione di Schroedinger stazionaria. Sotto, sotto, a grattare bene, l’esistenza delle curve di Zindler è garantita dalla esistenza di una gran quantità di integrali del moto, in termini meccanici, di quantità conservate dalla evoluzione dei tracciati delle biciclette in uno spazio funzionale, tutti esprimibili in termini geometrici come integrali di opportune combinazioni di curvatura, torsione e loro derivate. Quantità legate a forme di “elasticità generalizzata” di tali curve.
Vi sembrano parole senza senso? Non lo so. Spiegarle a fondo mi richiederebbe ore, mi richiederebbe di rituffarmi in quella scrivania, ripescare uno dei tanti progetti che non porterò mai a termine. Ma non sarebbe importante. Importante è avere imparato una lingua straniera che, come gli occhiali a raggi X delle pubblicità degli anni ’70, mi permette di vedere qualcosa di invisibile allo sguardo usuale. Non solo. Questo sguardo invisibile lo condivido, quotidianamente, con studenti e colleghi che come me si entusiasmano nella scoperta di legami profondi e impensati, gioiscono della esistenza di una trama segreta, si scambiano messaggi apparentemente codificati che parlano di questa bellezza nascosta. E’ di questa lingua comune e soprattutto della comunità che la parla di cui vado orgoglioso, che mi permette di indossare il mio magico copricapo di piume di struzzo che non è simbolo di diversità ma di appartenenza. Di questo, sotto il peso delle carte, gioisco.
Nicola Ciccoli
- S. Tabachnikov: Tire track geometry: variations on a theme. Israel Journal of Math. 151 (2004).
- M. Levi e S. Tabachnikov: On Bicycle Tire Tracks Geometry, Hatchet Planimeter, Menzin’s Conjecture, and Oscillation of Unicycle Tracks. Experimental Mathematics 18 (2009).
- R. Foote, M. Levi e S. Tabachnikov: Tractrices, bicycle tire tracks, hatchet planimeters, and a 100-year-old conjecture. Amer. Math. Monthly 120 (2013).
- M. Levi. Schrödinger’s equation and “bike tracks” – A connection. Journal of Geometry and Physics 115 (2014).
- G. Bor, M. Levi, R. Perline e S. Tabachnikov: Tire Tracks and Integrable Curve Evolution. International Mathematics Research Notices (2020).